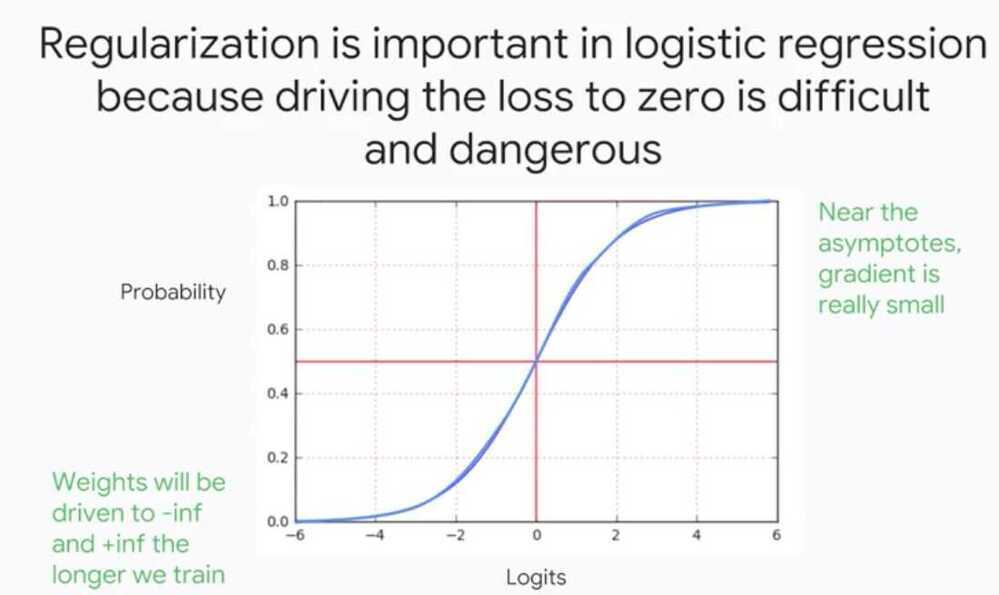
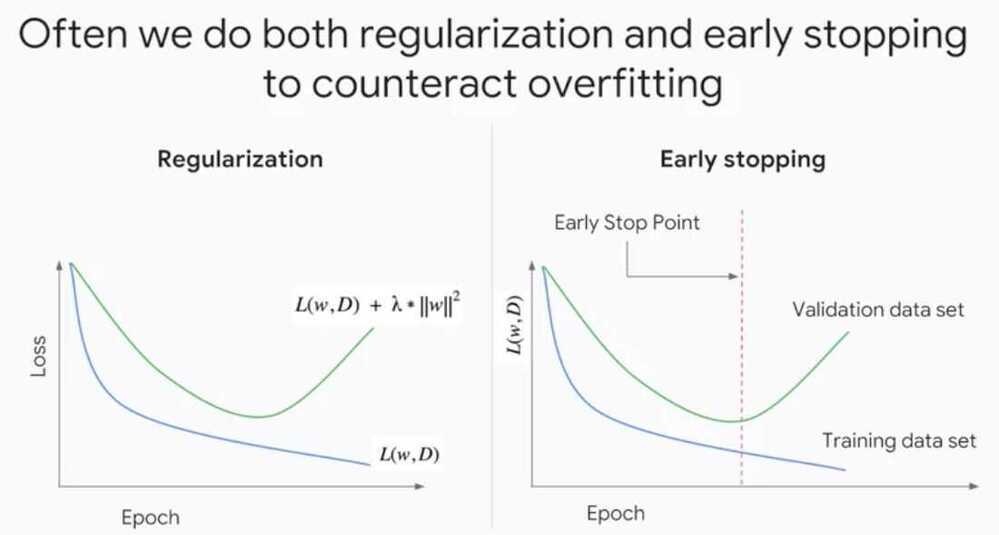
Regularization

Techniques used to generalize a model

Methods

• Early Stopping
• Parameter Norm Penalties
  • L1 regularization
  • L2 regularization
  • Max-norm regularization
• Dataset Augmentation
• Noise Robustness
• Sparse Representations

We use regularization method that penalize model complexity

Both L1 and L2 regularization techniques represent the model complexity as the magnitude of the weight vector, and try to keep that in check.

Magnitude of a vector is represented by the norm function

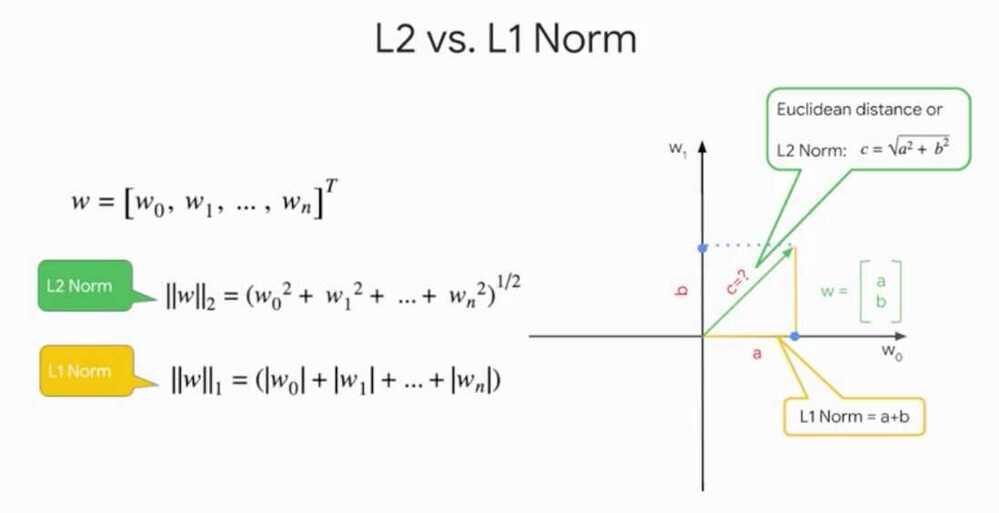
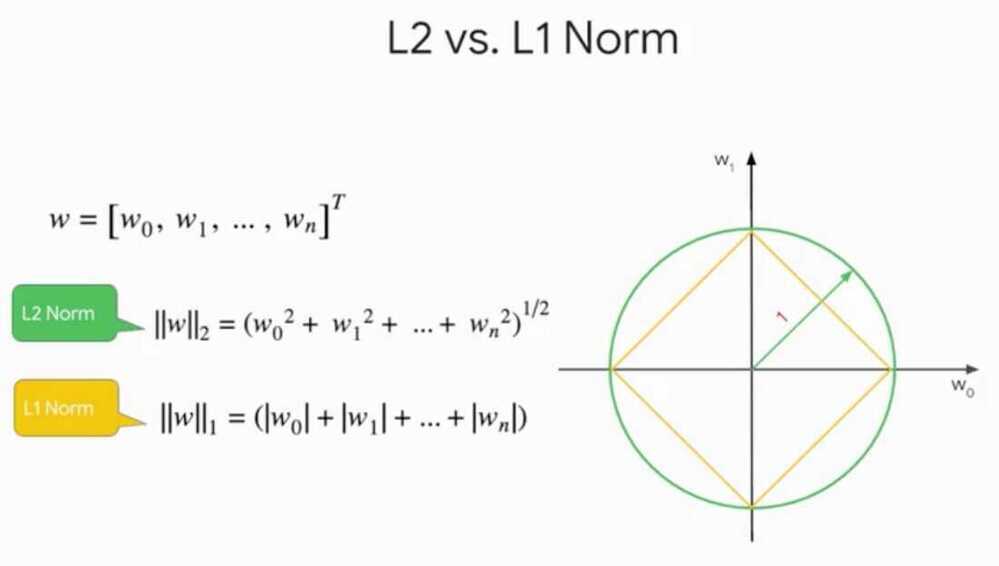
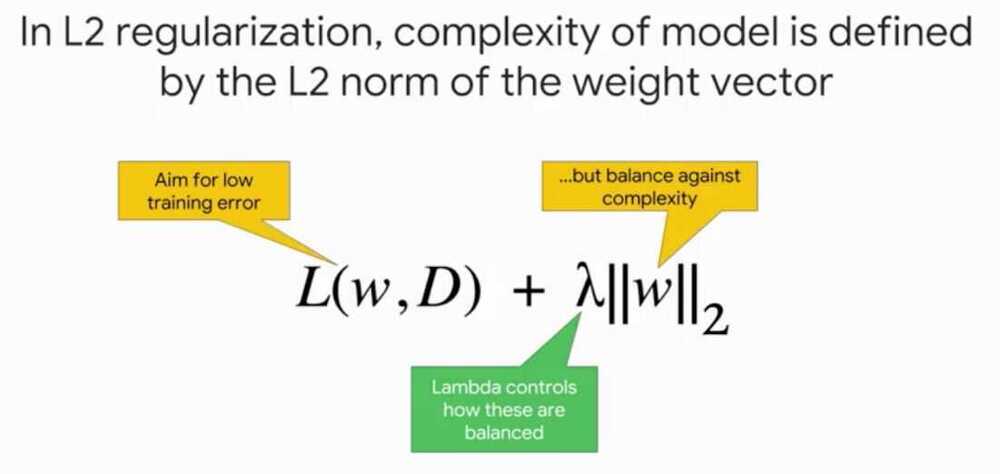
Here lambda, is a simple scalar value that allows us to control how much emphasis we want to put on model simplicity over minimizing training error.

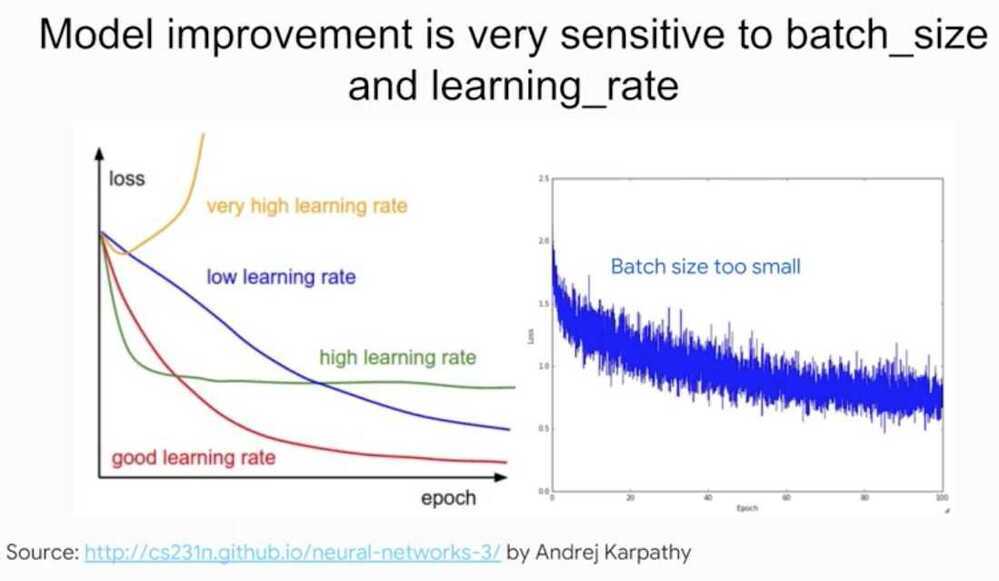
Learning Rate and Batch Size

By properly shuffling the dataset, you'll ensure each batch is representative of the entire dataset. Remember, the gradient are computed within the batch. If the batch is not representative, the loss will jump around too much from batch to batch.

Hyperparameter Tuning

• Differentiate between parameters and hyperparameters
• Think beyond simple grid search algorithms

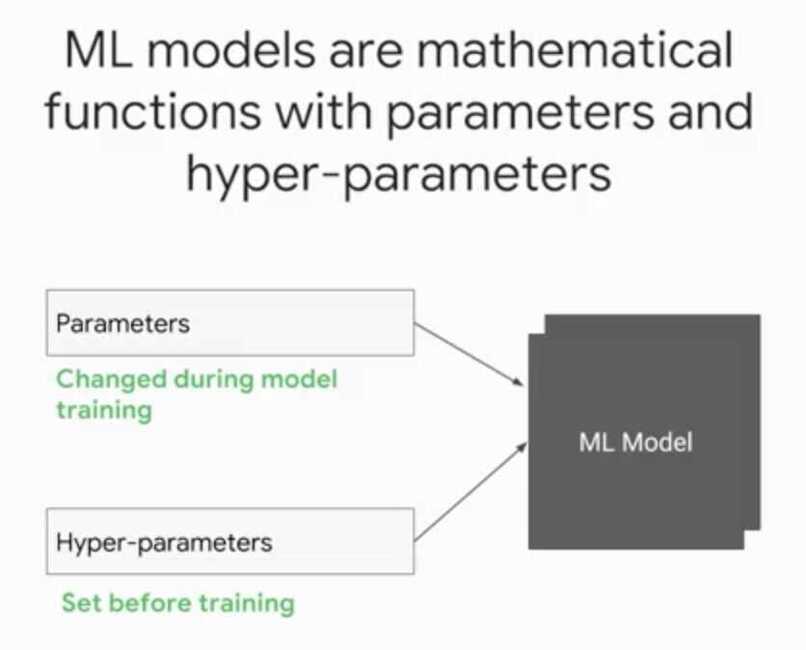
Parameter - real valued variable that changes during model training like all weights and biases

Hyperparameter - is a setting that we set before training and it doesn't change afterwards

• learning rate
• regularization rate
• batch size
• number of hidden layers in neural net
• number of neurons in each layer

There are a variety of model parameters too

• Size of model
• Number of hash buckets
• Embedding size

Wouldn't it be nice to have the NN training loop do meta-training across all these parameters

How to use Cloud ML Engine for hyperparameter tuning

1. Make the parameter a command-line argument

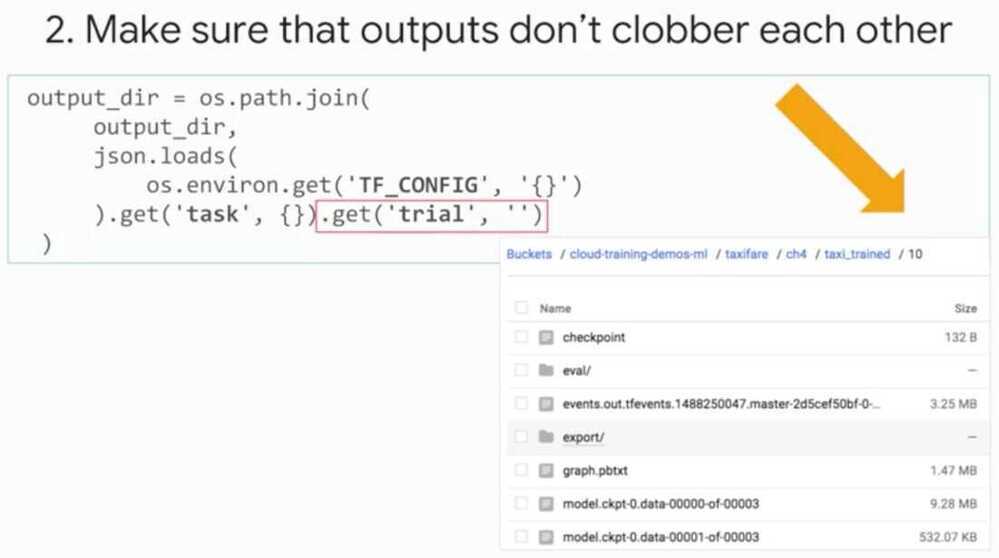
2. Make sure outputs don't clobber each other

3. Supply hyperparameters to training job

• Regularization for sparsity
• Logistic regression
• Introduction to Neural Networks
• Training Neural Networks

Regularization for Sparsity

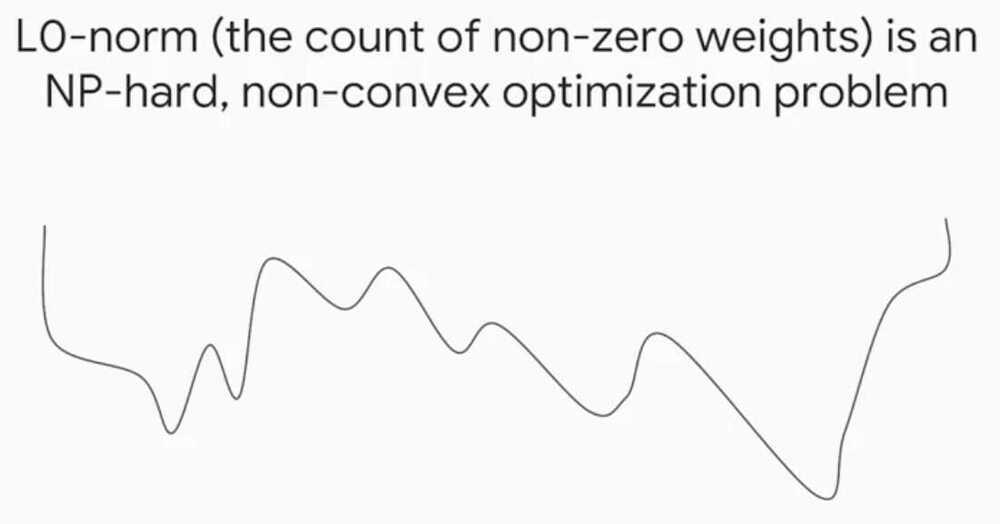
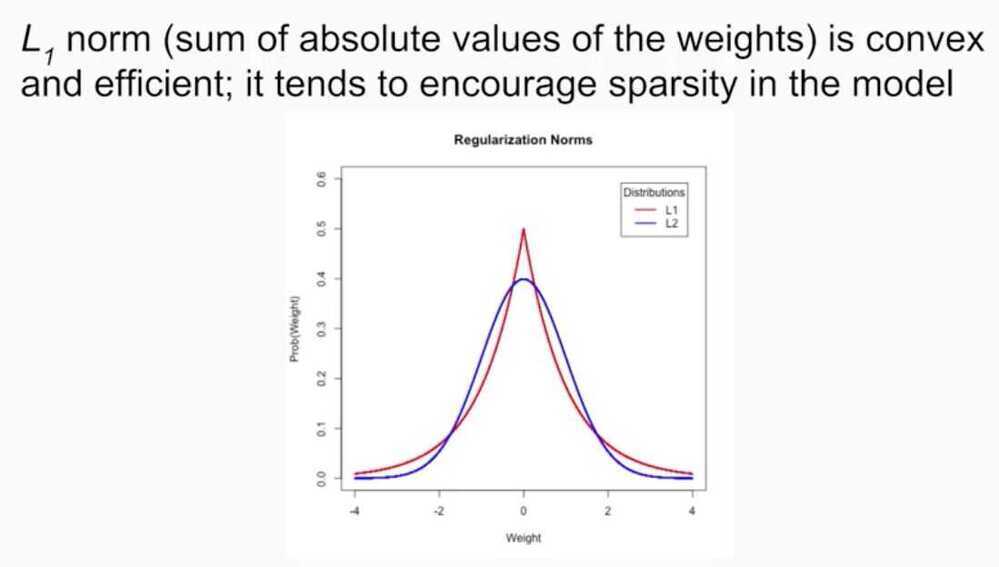
Some other norms or the L0 norm that we already covered which is the count of the non-zero values in a vector, and the L infinity norm which is the maximum absolute value of any value in a vector. In practice though, usually the L2-norm provides more generalizable models and the L1 norm. However, we will end up with much more complex heavy models if we use L2 instead of L1. This happens because often features have high correlation with each other, and L1 regularization which use one of them and throw the other away, whereas L2 regularization will keep both features and keep their weight magnitudes small.So with L1, you can end up with a smaller model but it may be less predictive.Is there any way to get the best of both worlds?

The elastic net is just a linear combination of the L1 and L2 regularizing penalties.This way, you get the benefits of sparsity for really poor predictive features whilealso keeping decent and great featureswith smaller weights to provide a good generalization.The only trade off now is there aretwo instead of one hyper parameters totune with the two different Lambda regularization parameters.

https://goo.gl/281mPF

Question

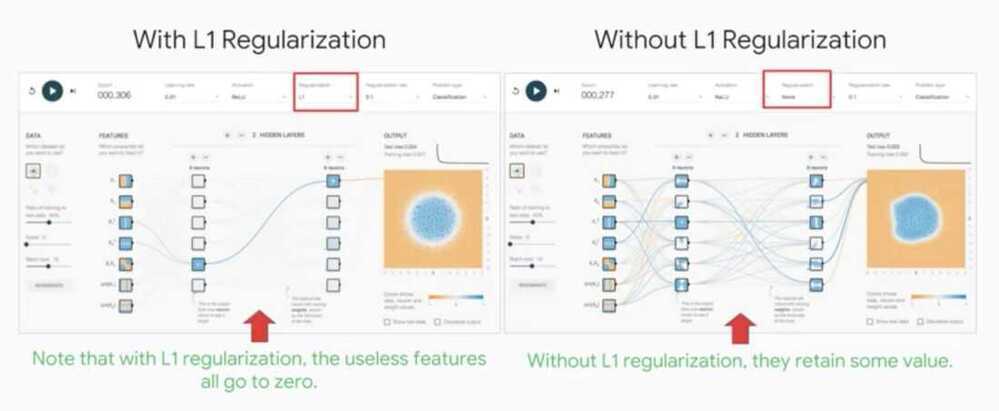
1. Which type of regularization is more likely to lead to zero weights? - L1
2. Which type of regularization penalizes large weight values more? - L2

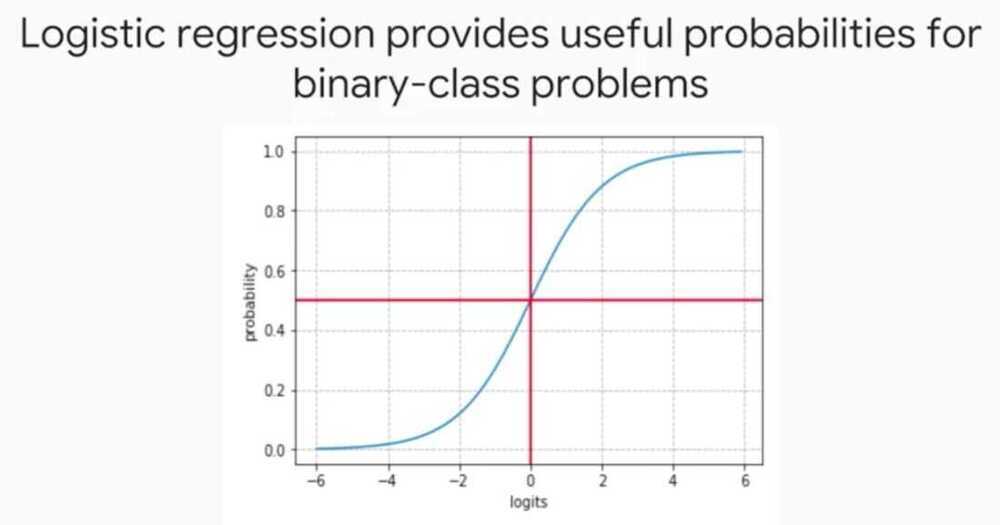
Logistic Regression

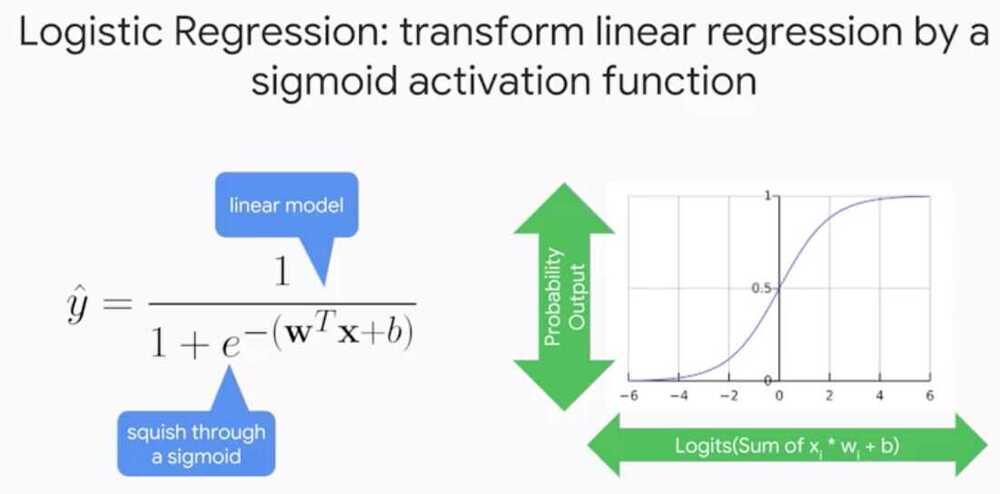
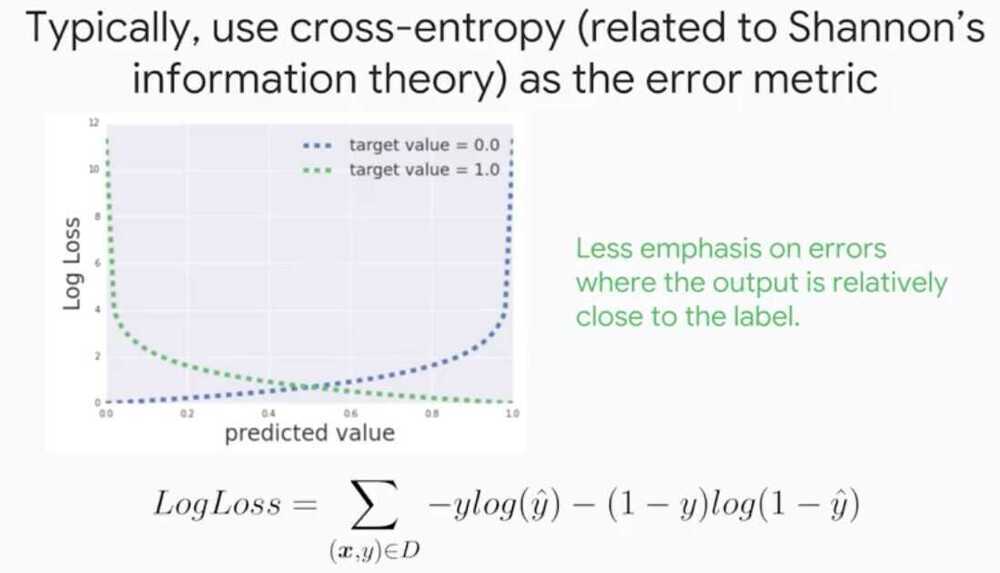
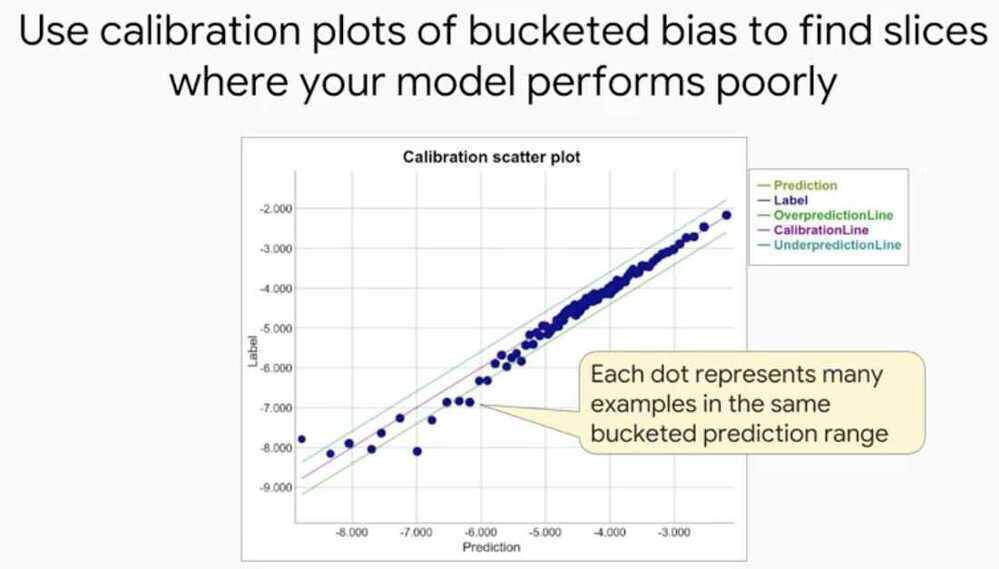
Introduction to Neural Networks

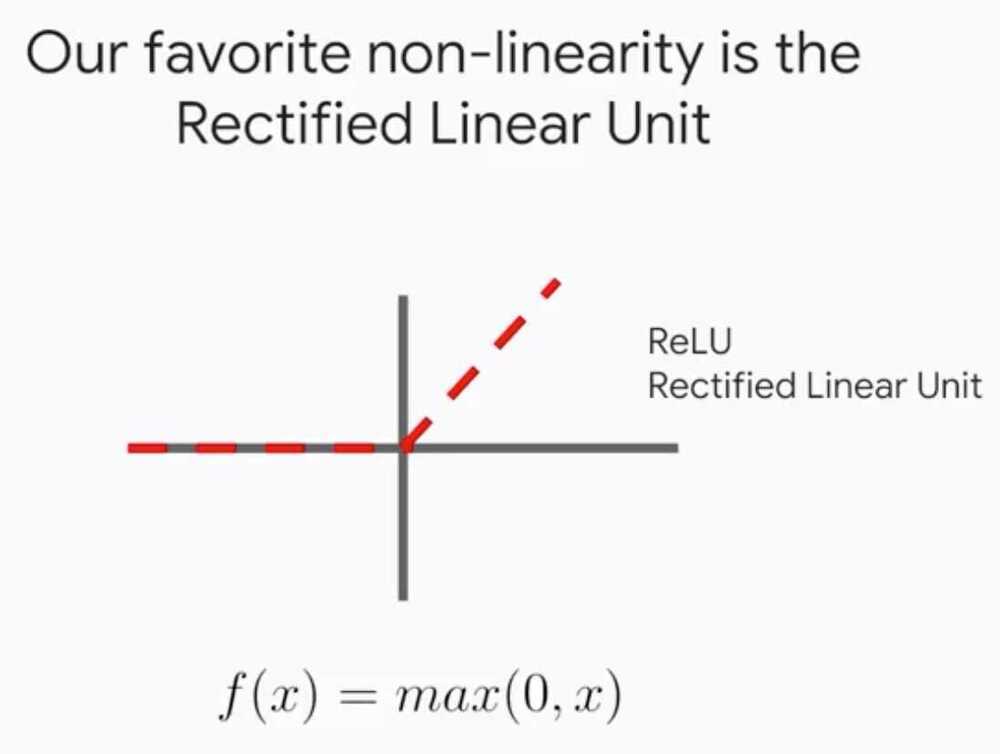
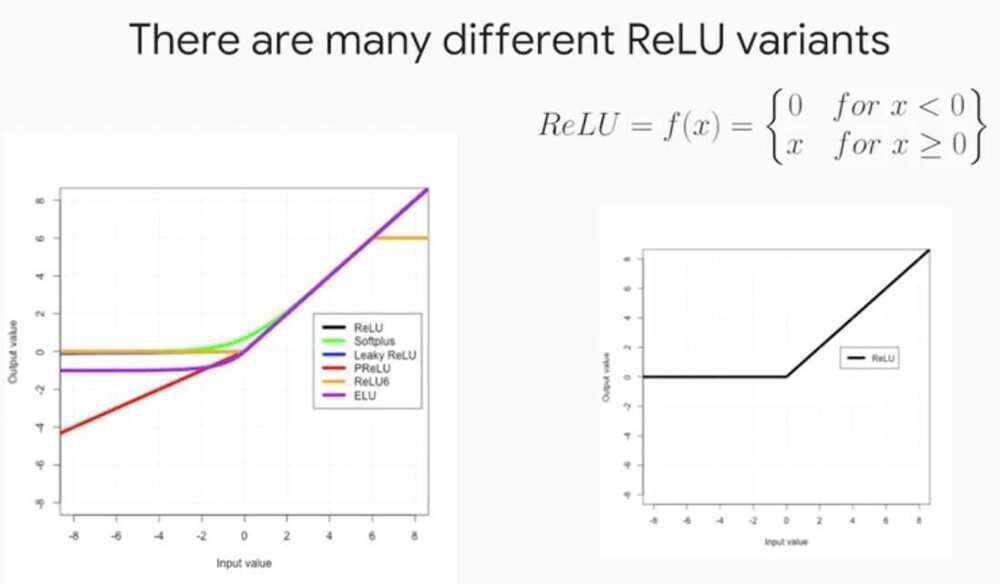
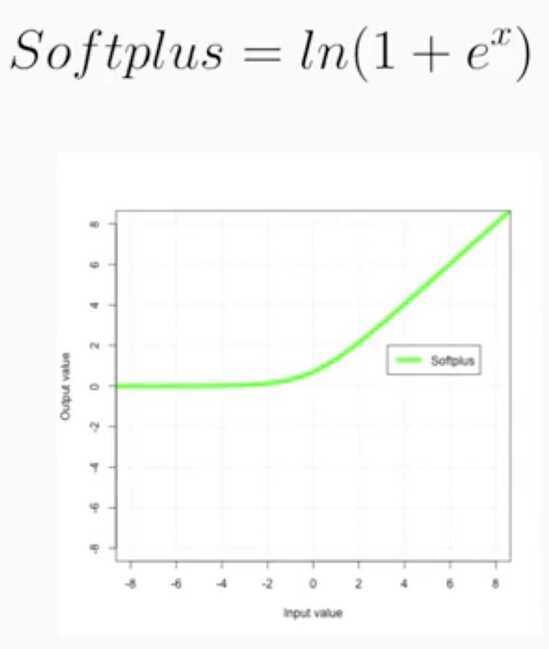
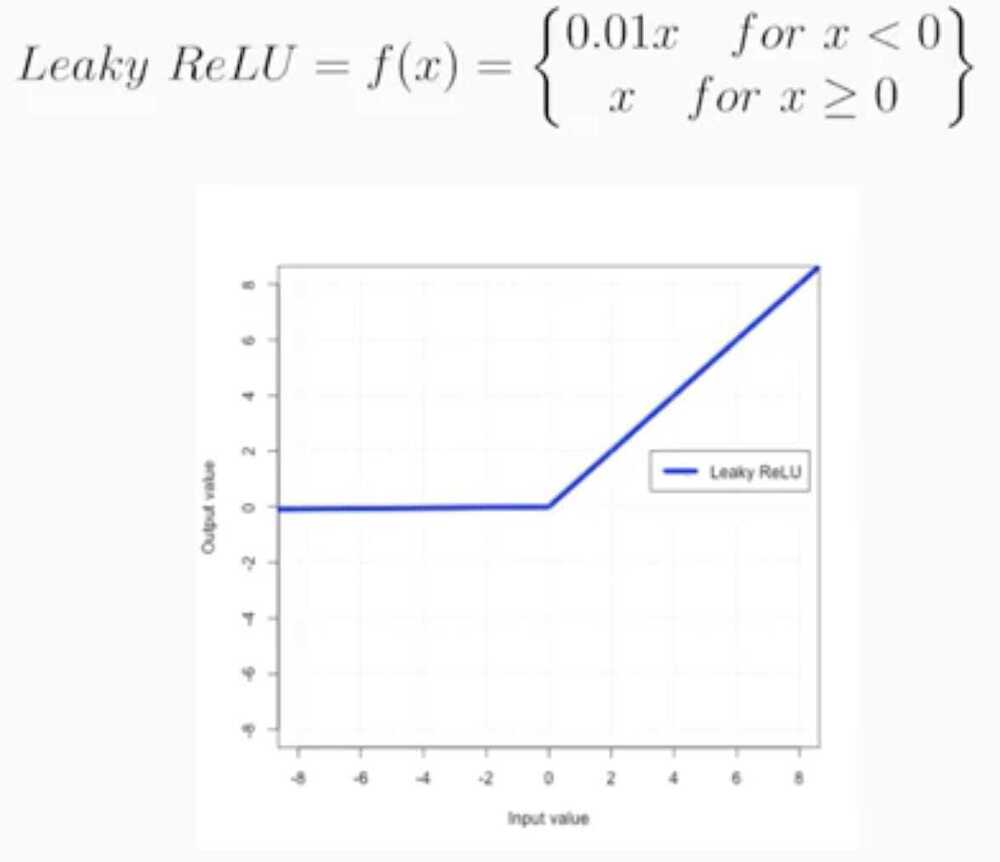
Parametric ReLU

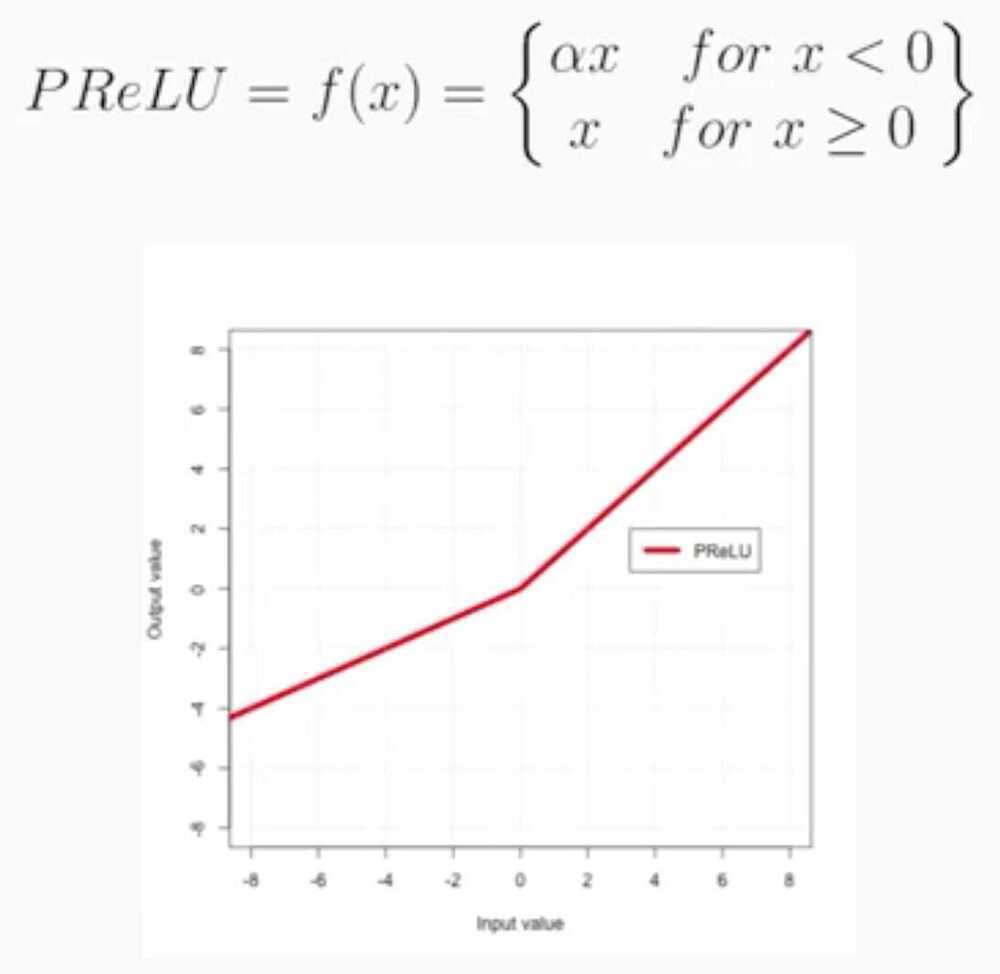
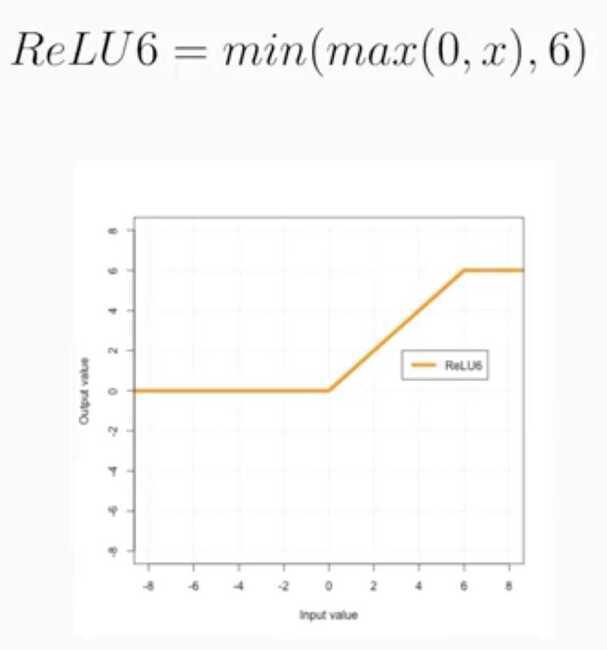
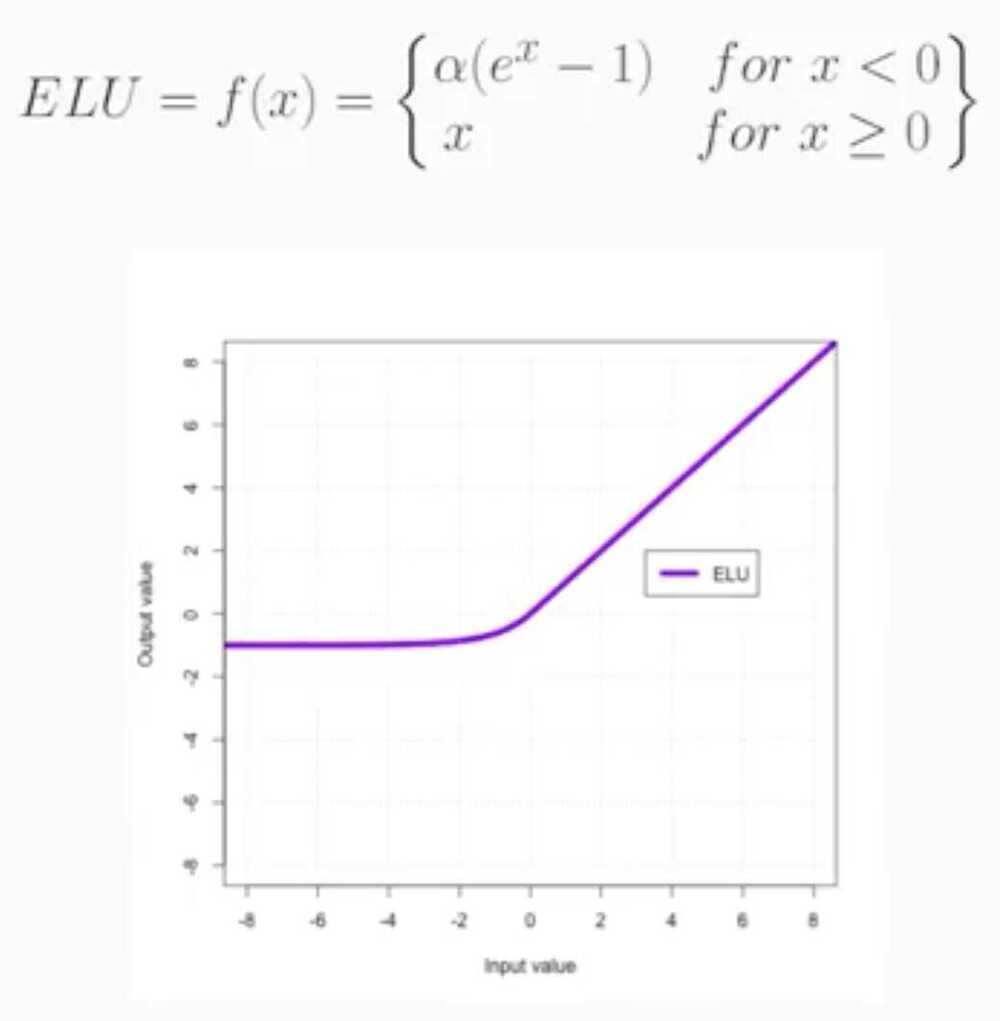
Exponential Linear Unit

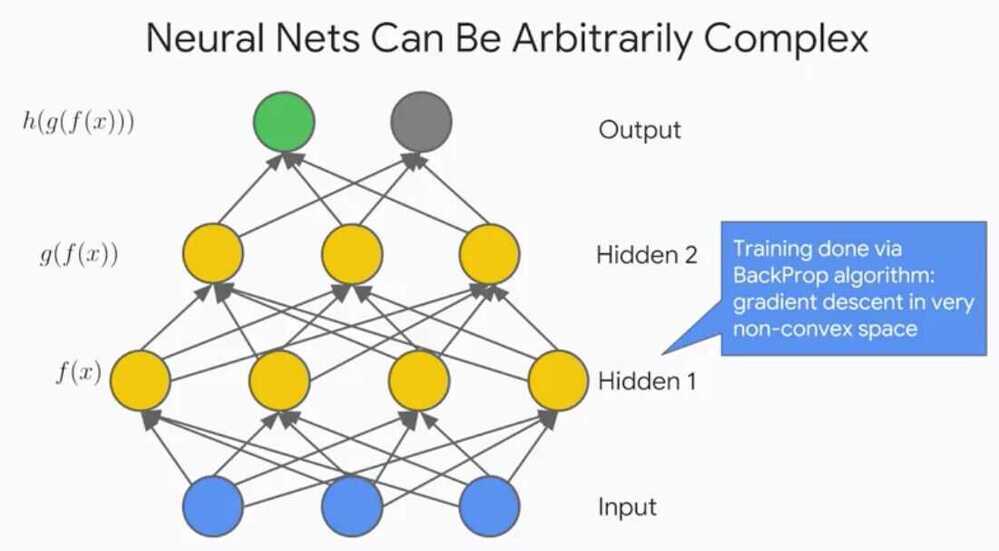
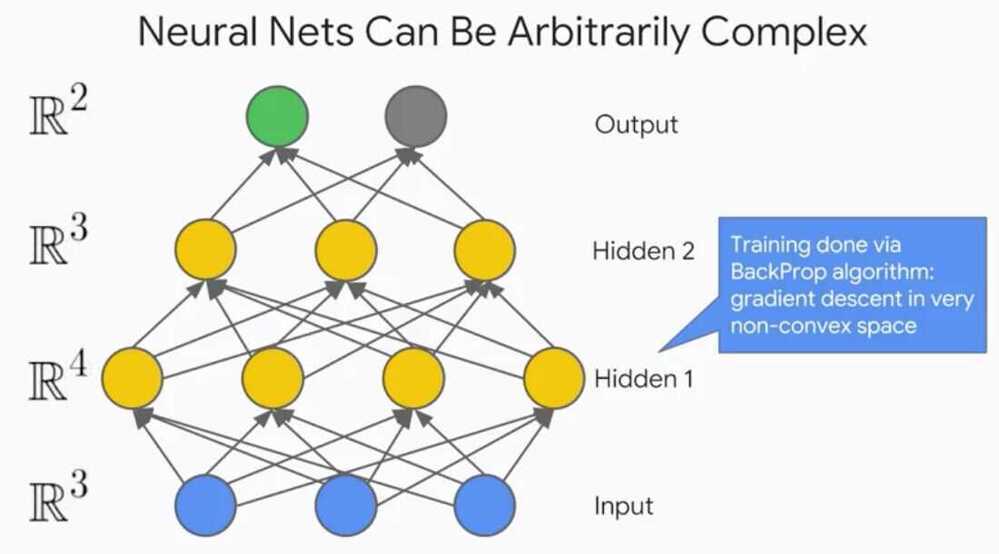
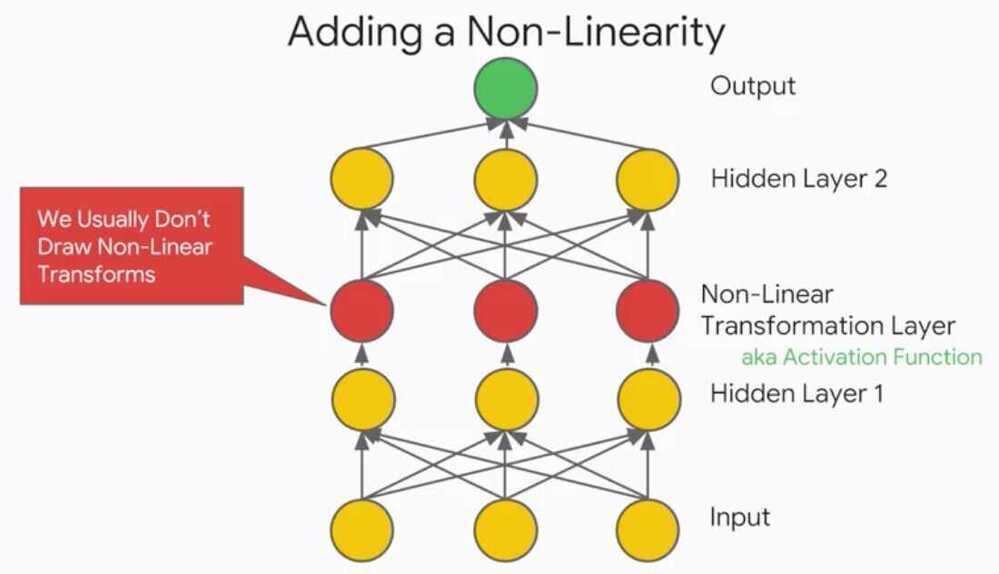
Neural networks can be arbitrarily complex, there can be many layers, neurons per layer, outputs, inputs, different types activation functions et cetra.

What does the purpose of multiple layers?Each layer I add, adds the complexity of the functions I can create.Each subsequent layer is a composition of the previous functions.Since we are using nonlinear activation functions in my hidden layers, I'm creating a stack of data transformations that rotate, stretch and squeeze my data.Remember, the purpose of doing all of this isto transfer my data in such a way that can nicelyfit hyper plane to it for regression orseparate my data with a hyper planes for classification.We are mapping from the original feature space to some new convoluted feature space.

What does adding additional neurons to a layer do?Each neuron I add, adds a new dimension to my vector space.If I begin with three input neurons, I start in R3 vector space.But if my next layer has four neurons that I moved to an R4 vector space.Back when we talked about Kernel methods in our previous course, we had a data set that couldn't be easily separatedwith a hyper plane in the original input vector space.But, by adding the dimension and then transformthe data to fill that new dimension in just the right way, we were then easily able to make a clean slice between the classes of data.The same applies here with neural networks.

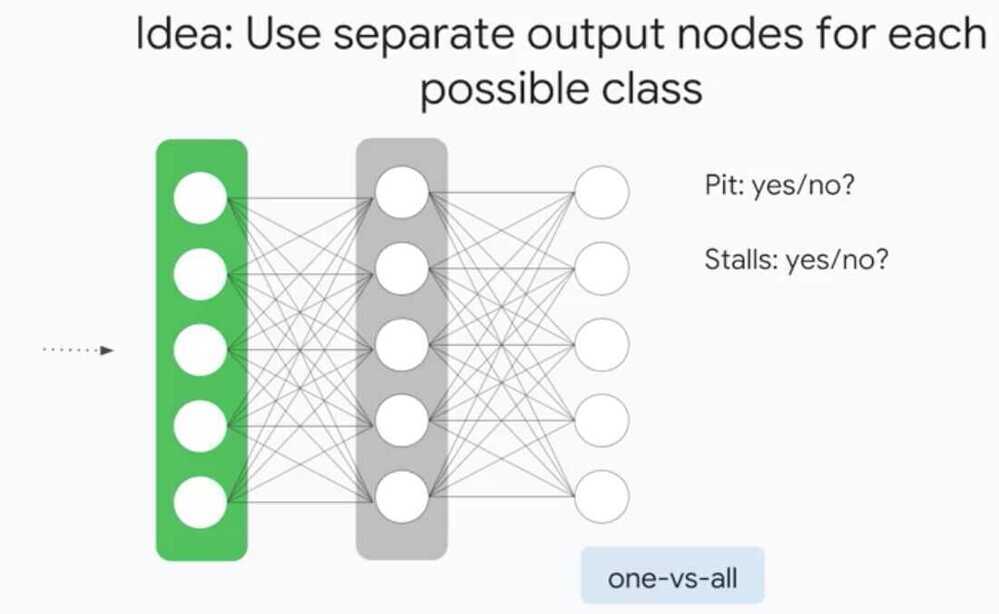
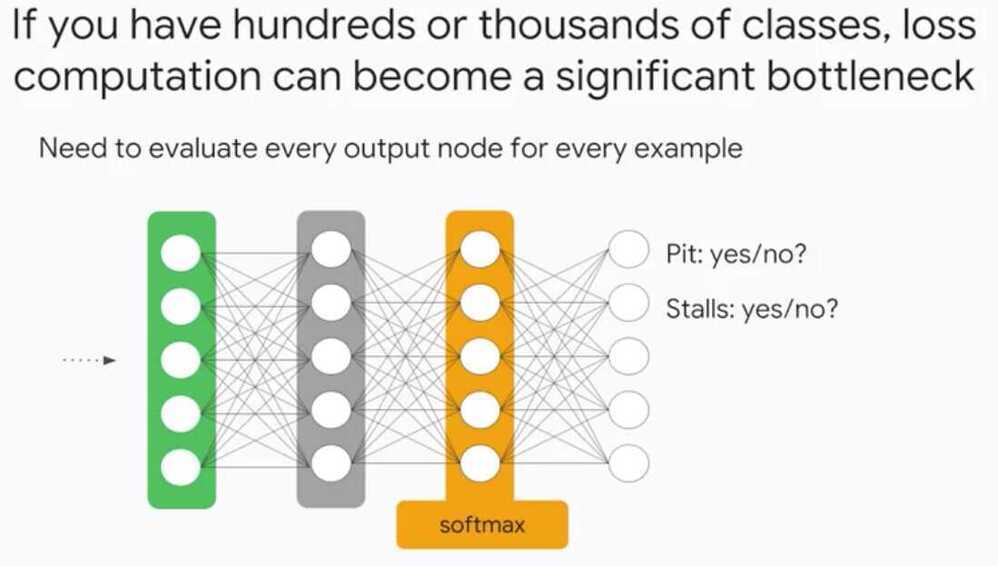
What might having multiple output nodes do?Having multiple output nodes allows you tocompare to multiple labels and then propagate the corresponding areas backwards.You can imagine doing image classification where there aremultiple entities or classes within each image.We can't just predict one class because there maybe many, so having this flexibility is great.

Training Neural Networks

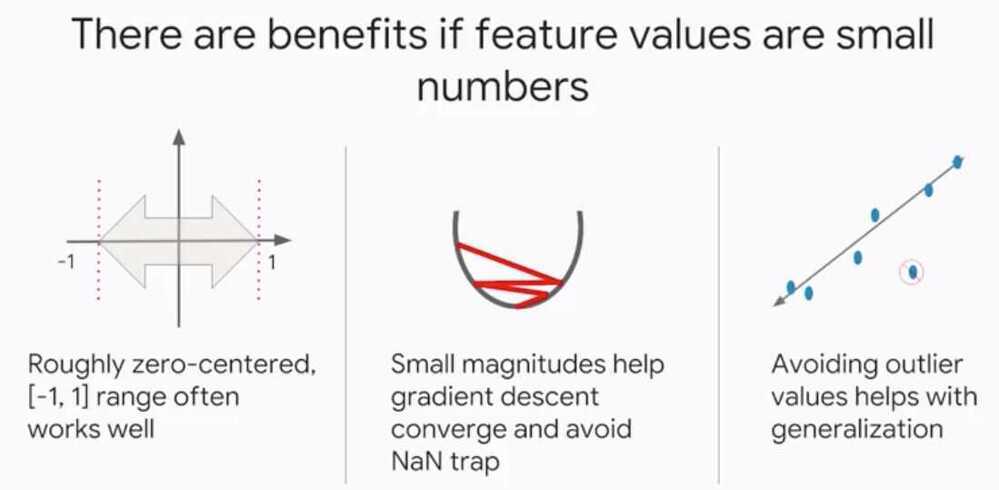
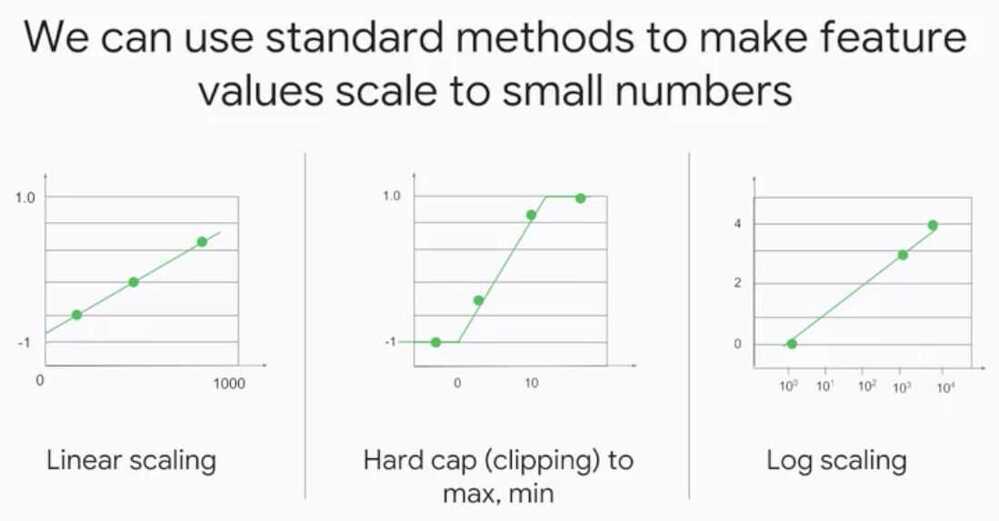
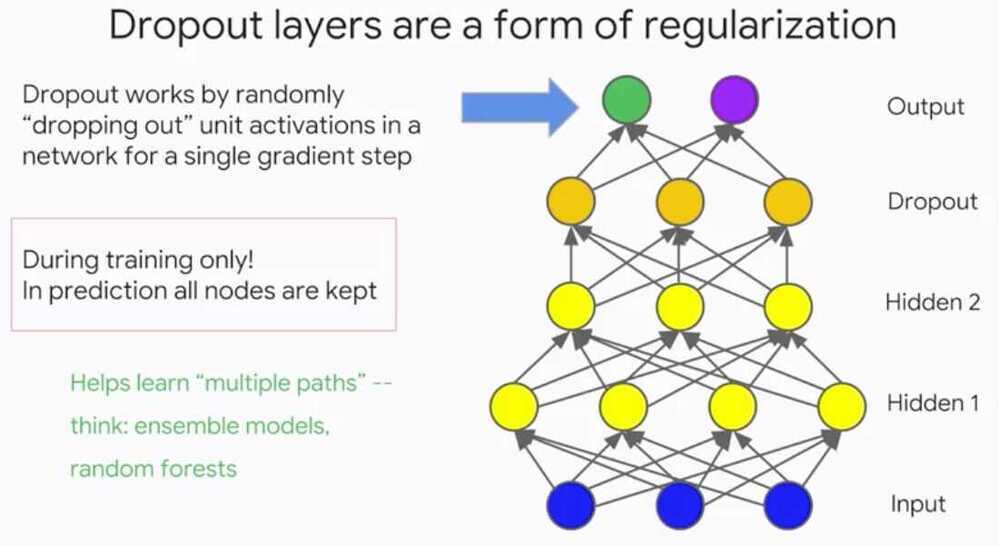
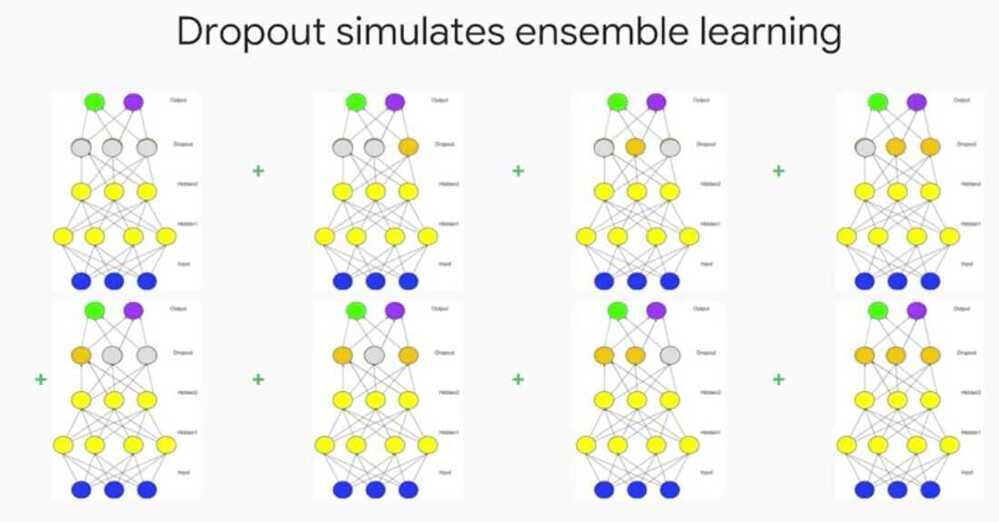
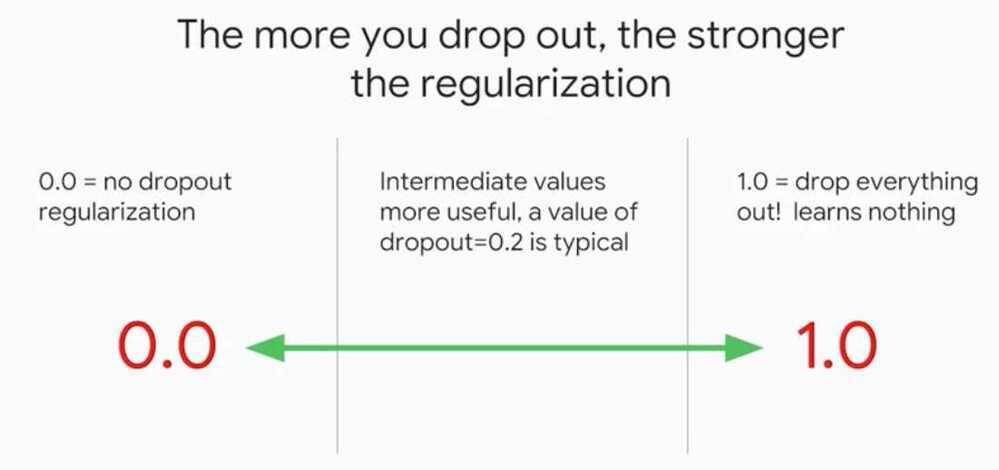
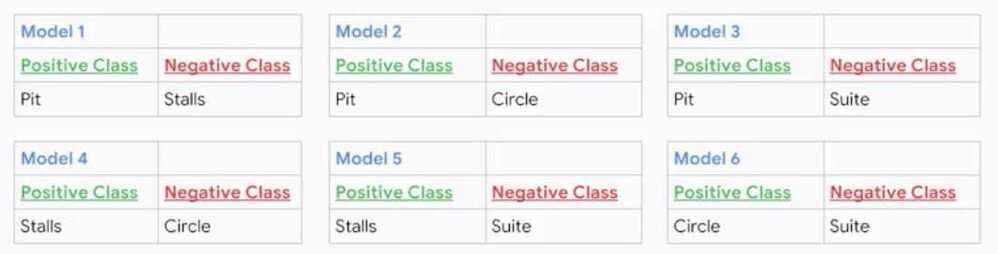
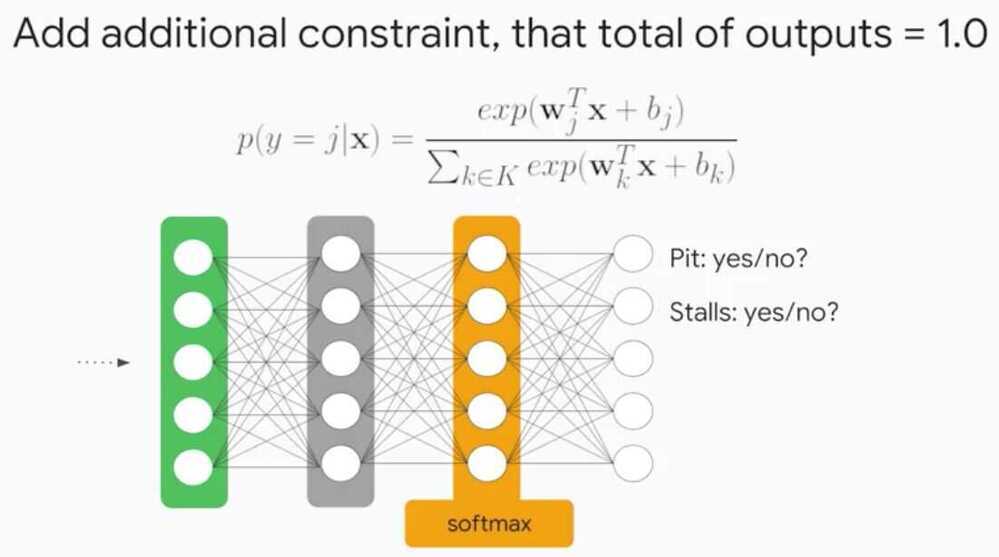
Multi-Class Neural Networks