Non linear regression
Non-linear Regression
- We can generalize further to models that are nonlinear:
where the g's are non-linear functions
- In statistics this is referred to as a generalized linear regression
- Closed form (analytical) solutions are rare
- We have a multivariate non-linear optimization problem
Optimization in the Non-Linear Case
- We seek the minimum of a function in d dimensions, where d is the number of parameters (d could be large)
- There are a multitude of heuristic search techniques
- Steepest descent (follow the gradient)
- Newton methods (use 2nd derivative information)
- Conjugate gradient
- Line search
- Stochastic search
- Genetic algorithms
- Two cases
- Convex (nice -> means a single global optimum)
- Non-convex (multiple local optima -> need multiple starts)
Other non-linear models
- Splines
- Patch together different low-order polynomials over different parts of the x-space
- Works well in 1 dimension, less well in higher dimensions
- Memory-based models
- Local linear regression
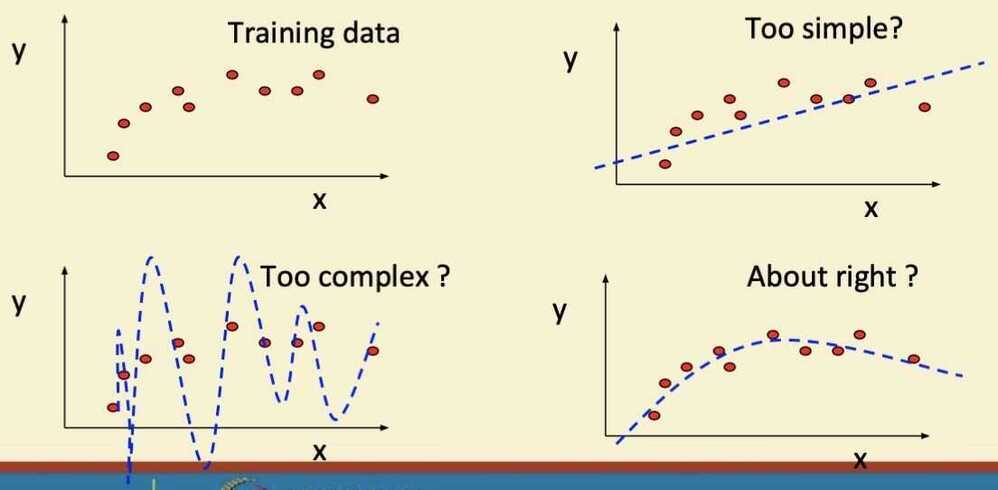
Complexity vs Goodness of Fit
Generalized Linear Models (GLMs)

Tree-Structured Regression
- Functional form of model is a "regression tree"
- Univariate thresholds at internal nodes
- Constant or linear surfaces at the leaf nodes
- Yields piecewise constant (or linear) surface
- (like classification tree, but for regression)
- Very crude functional form... but
- Can be very useful in high-dimensional problems
- Can useful for interpretation
- Can handle combinations of real and categorical variables
- Search problem
- Finding the optimal tree is intractable
- Practice: greedy algorithms
Model Averaging / Ensembles
- Can average over parameters and models
- E.g., weighted linear combination of predictions from multiple models
y = Σ wk yy
- Why? Any predictions from a point estimate of parameters or a single model has only a small chance of the being the best
- Averaging makes our predictions more stable and less sensitive to random variations data set (good for less stable models like trees)