Skip to main content

Association Rules & Apriori Algorithm

Association Rule Mining​

  • Given a set of transactions, find rules that will predict the occurrence of an item based on the occurrences of other items in the transaction

image

Definition: Frequent Itemset​

  • Itemset
    • A collection of one or more items
      • Example: {Milk, Bread, Diaper}
    • k-itemset
      • An itemset that contains k items
  • Support count (σ)
    • Frequency of occurrence of an itemset
    • E.g. σ({Milk, Break, Diaper}) = 2
  • Support
    • Fraction of transactions that contain an itemset
    • E.g. s({Milk, Bread, Diaper}) = 2/5
  • Frequent Itemset
    • An itemset whose support is greater than or equal to a minsup threshold
  • Association Rule
    • An implication expression of the form X->Y, where X and Y are itemsets
    • Example
      • {Milk, Diaper} -> {Beer}
  • Rule Evaluation Metrics
    • Support (s)
      • Fraction of transactions that contain both X and Y
    • Confidence (c)
      • Measures how often items in Y appear in transactions that contain X
    • Example

image

Association Rule Mining Task​

  • Given a set of transactions T, the goal of association rule mining is to find all rules having
    • support >= minsup threshold
    • confidence >= minconf threshold
  • Brute-force approach
    • List all possible association rules
    • Compute the support and confindence for each rule
    • Prune rules that fail the minsup and minconf thresholds
    • Computationally prohibitive

Mining Association Rules​

  • Two-step approach

    1. Frequent Itemset Generation

      • Generate all itemsets whose support >= minsup

    2. Rule Generation

      • Generate high confidence rules from each frequent itemset, where each rule is a binary partitioning of a frequent itemset

  • Frequent itemset generation is still computationally expresive

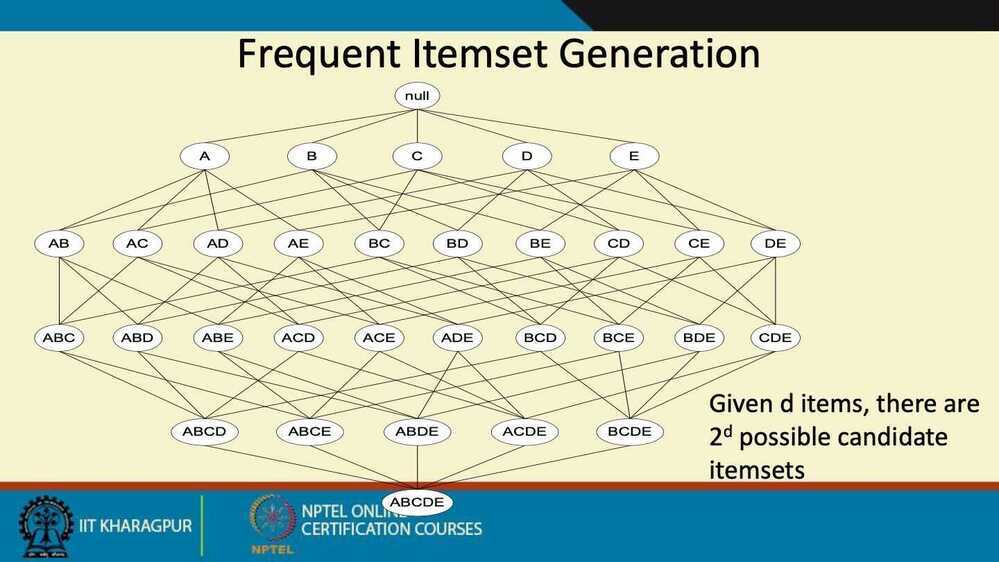
image

image

Frequent Itemset Generation Strategies​

  • Reduce the number of candidates (M)
    • Complete search: M = 2^d^
    • Use pruning techniques to reduce M
  • Reduce the number of transactions (N)
    • Reduce size of N as the size of itemset increases
    • Used by DHP and vertical-based mining algorithms
  • Reduce the number of comparisons (NM)
    • Use efficient data structures to store the candidates or transactions
    • No need to match every candidate against every transaction

DHP - Direct Hashing and Pruning

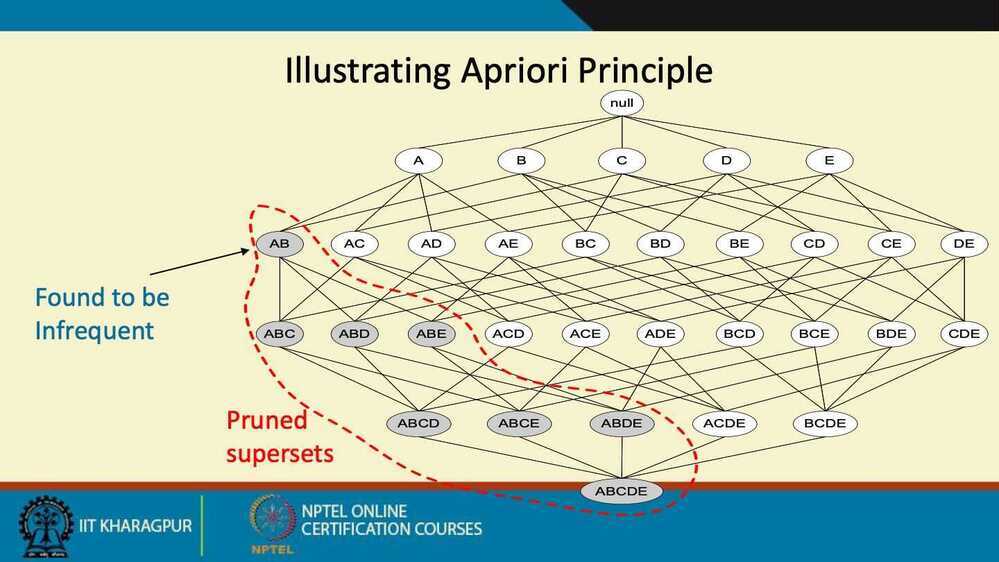
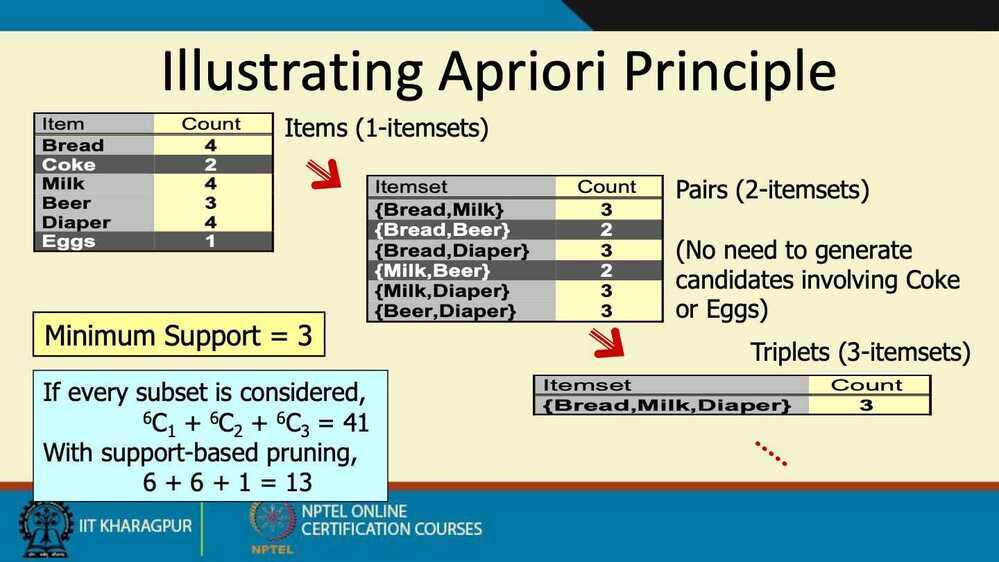
image

Example - If bat + ball are not frequent, then we can say that bat + ball + gloves is also not frequent.

Other way around of Apriori principle - if an itemset is not frequent, then all its superset are also not frequent.

image

image

Apriori Algorithm​

  • Let k = 1
  • Generate frequent itemsets of length 1
  • Repeat until no new frequent itemsets are identified
    • Generate length (k+1) candidate itemsets from length k frequent itemsets
    • Prune candidate itemsets containing subsets of length k that are infrequent
    • Count the support of each candidate by scanning the DB
    • Eliminate candidates that are infrequent, leaving only those that are frequent

Factors affecting complexity​

  • Choice of minimum support threshold
    • Lowering support threshold results in more frequent itemsets
    • this may increase number of candidates and max length of frequent itemsets
  • Dimensionality (number of items) of the data set
    • more space is needed to store support count of each item
    • if number of frequent items also increases, both computation and I/O costs may also increase
  • Size of database
    • Apriori makes multiple passes, run time of algorithm increase with number of transactions
  • Average transaction width
    • This may increase max length of frequent itemsets and traverals of hash tree (number of subsets in a transaction increases with its width)