Andrew NG

Model and cost function

1. Model representation - Linear regression using Training set

m - number of training examples

x's - input variables / features

y's - output variable / "target" variable

(x,y) - one training example

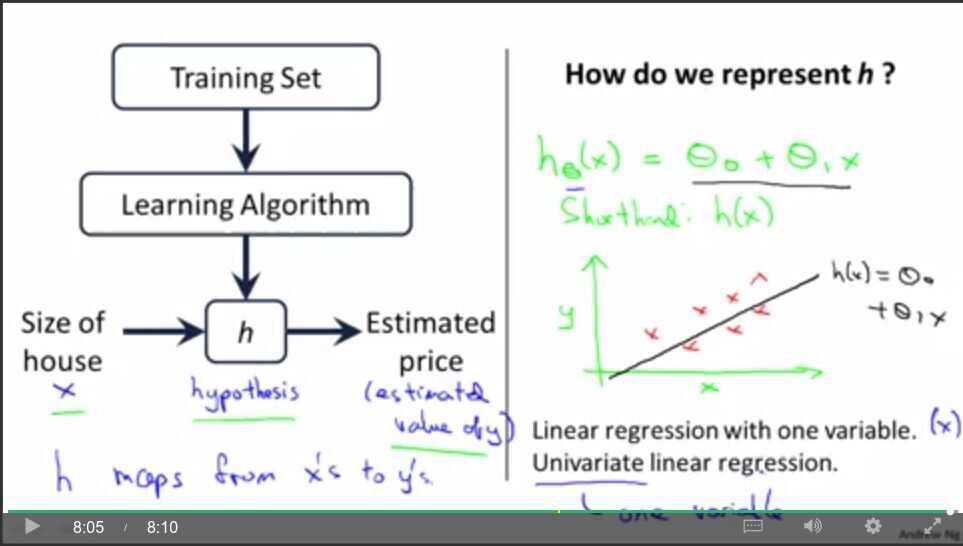
2. Cost function

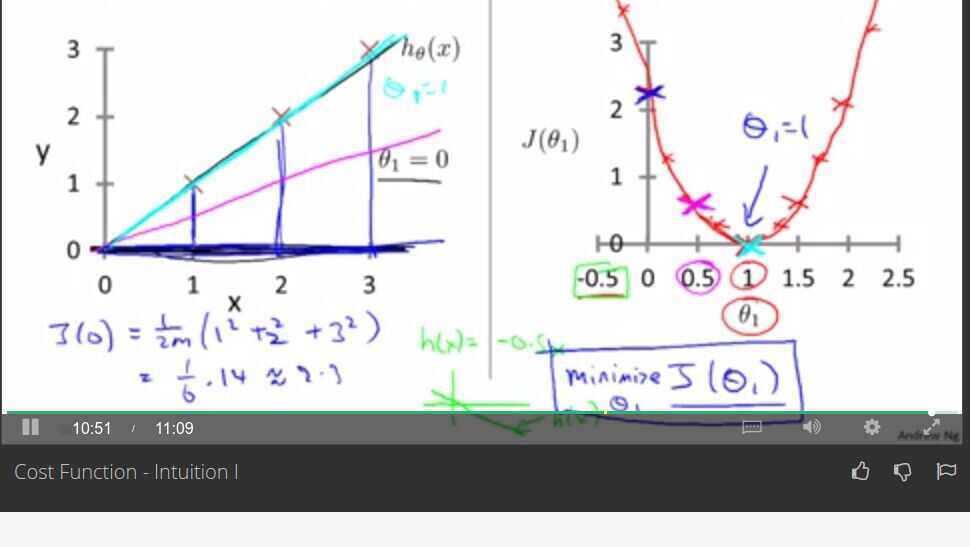
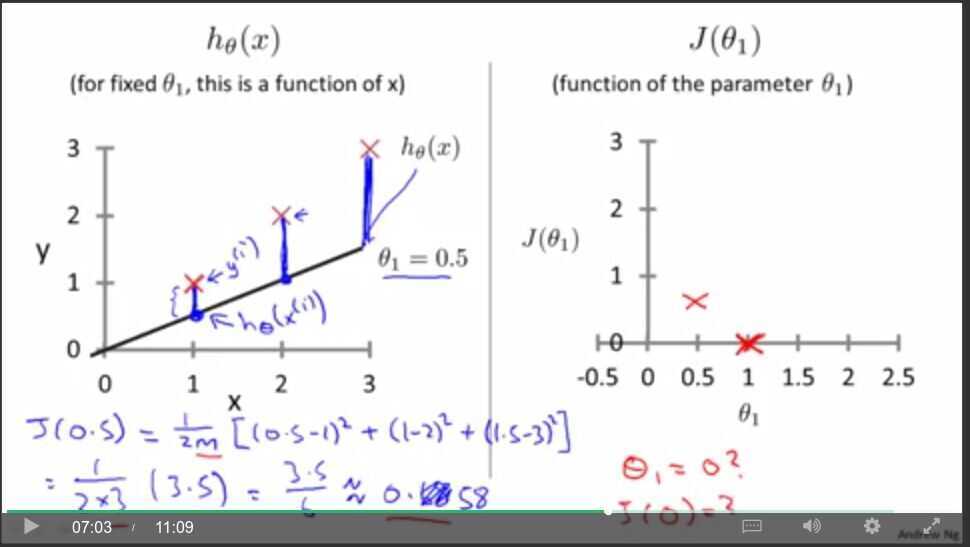
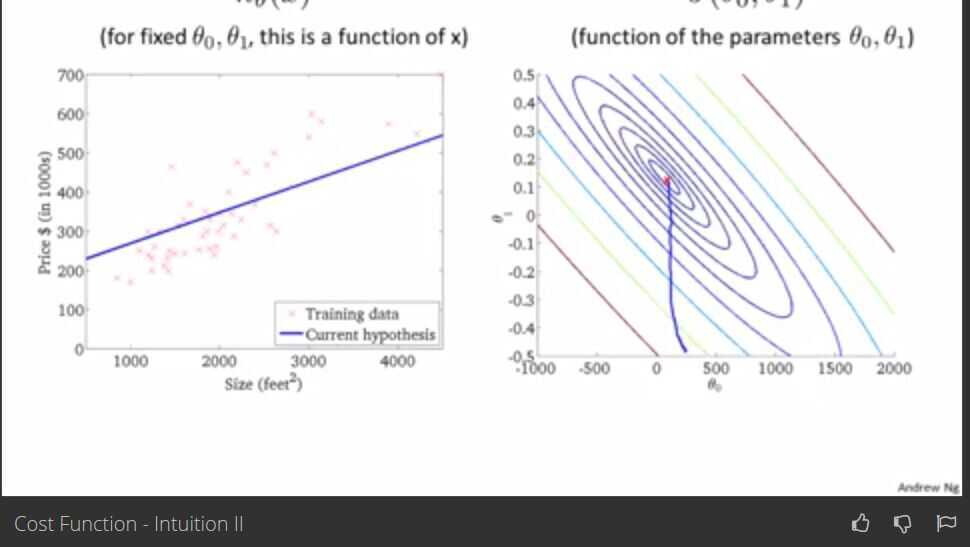
Cost function intuition -

Octave

• Singular Value Decomposition (SVD)

Every nxm matrix can be written as a product of three smaller matrices.

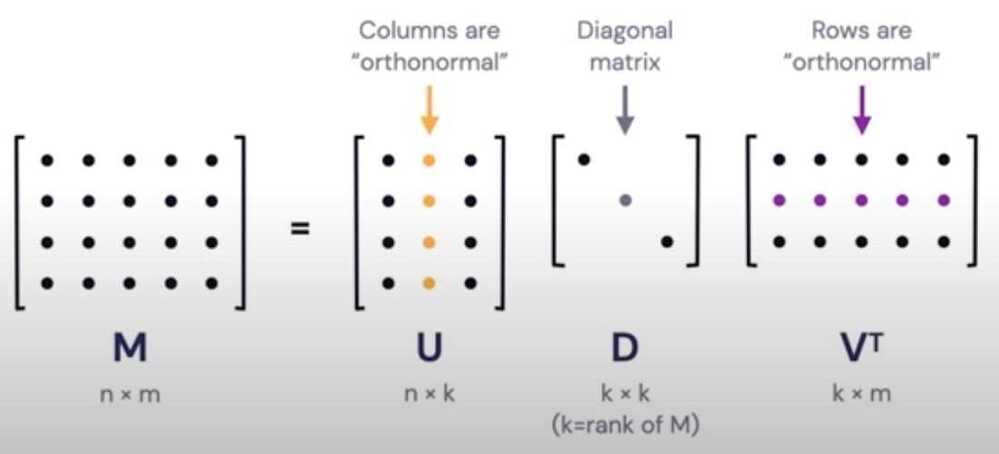
• SVD appreas in lots of places
  • Statistics (PCA)
  • Chemical physics
  • Image processing
  • Genomics
  • Robotics
  • Quantum physics (entanglement)
  • Data embeddings / vector embeddings

Gradient Descent for Linear regression with one variable

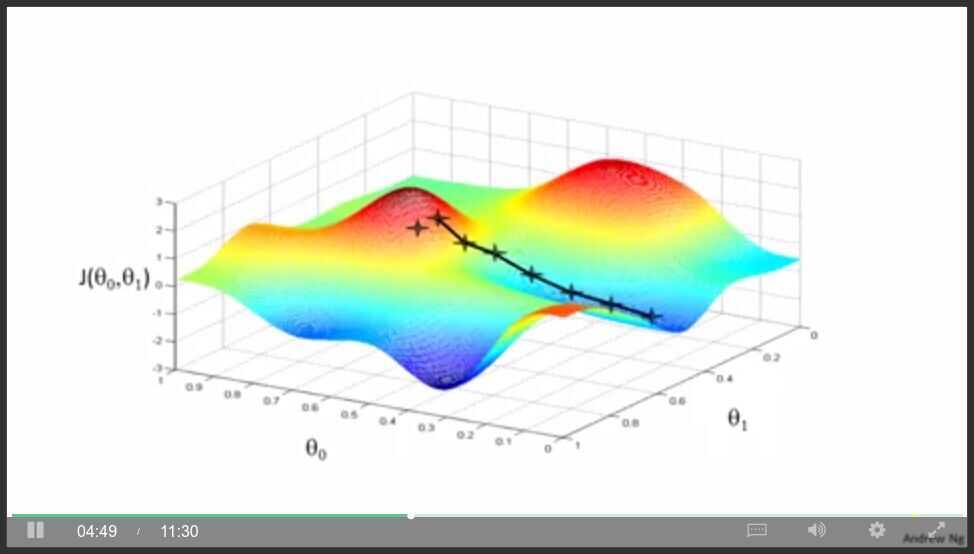
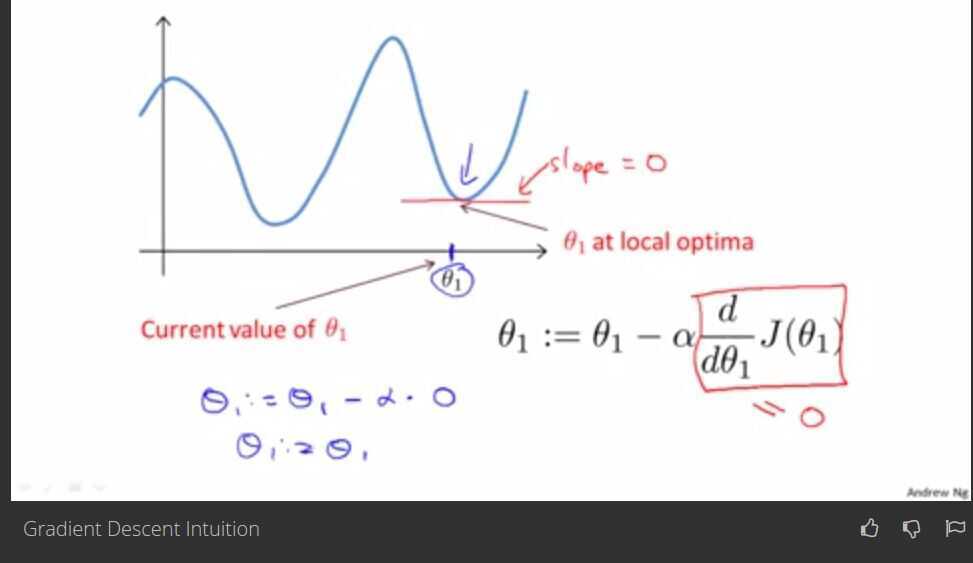
Gradient descent intuition

Derivative term

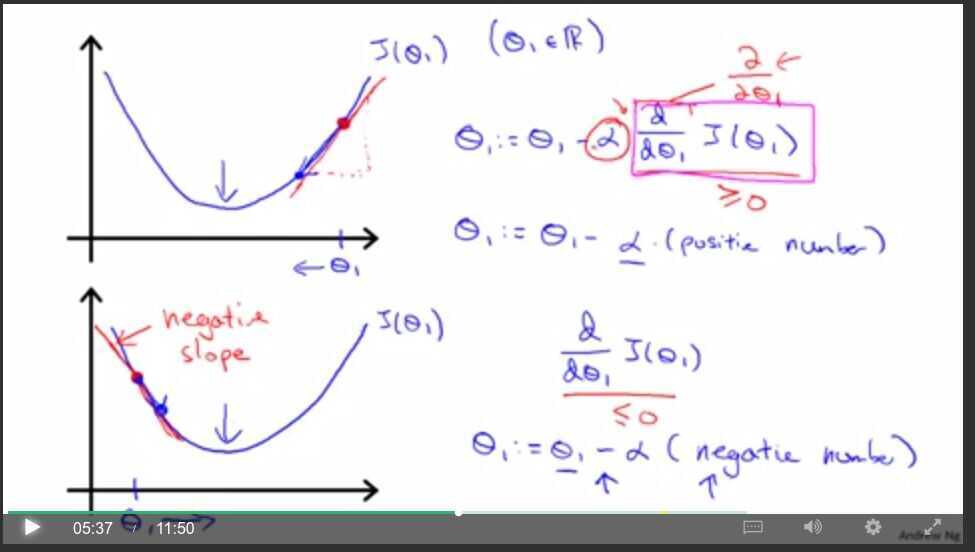
Alpha

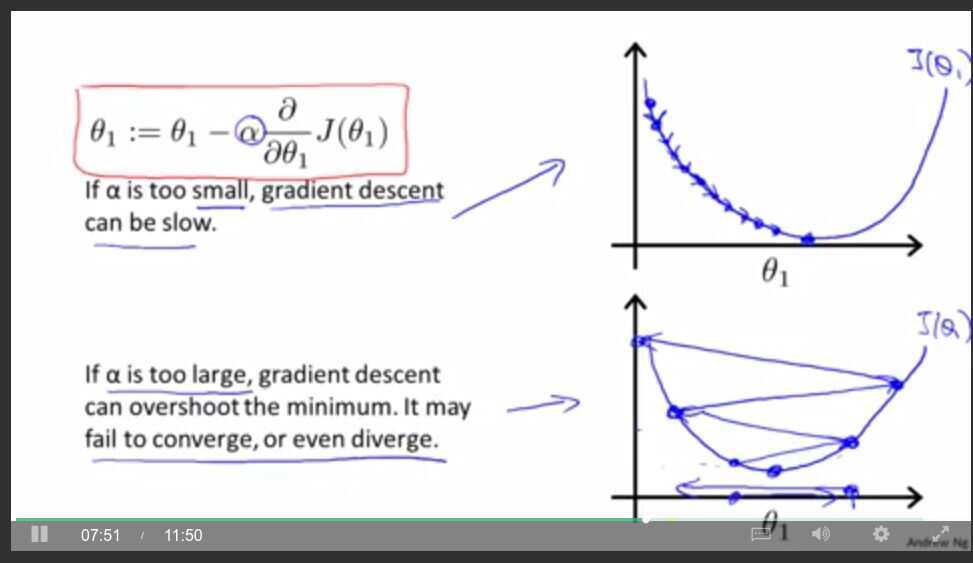
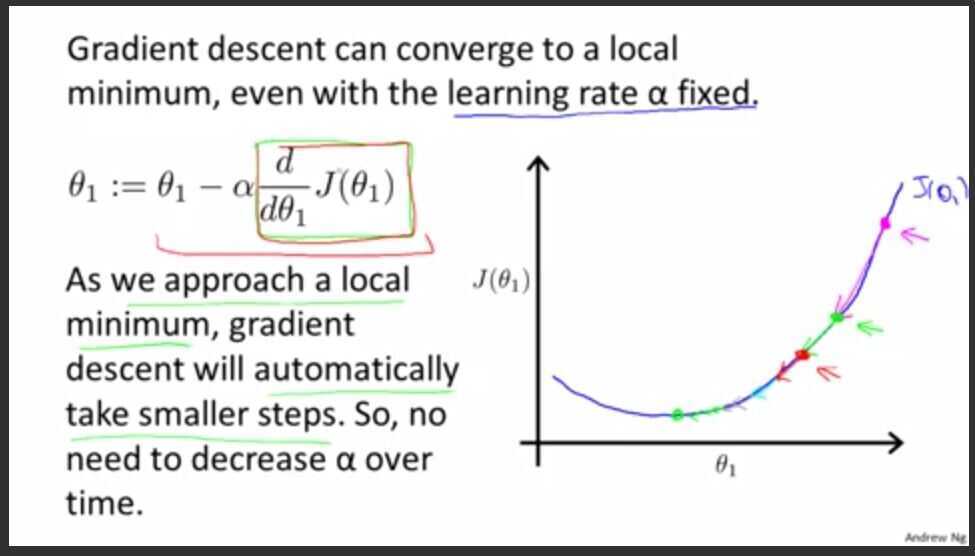
Gradient Descent for Linear Regression

Gradient descent is a convex function (Global minimum)

Also called (Batch gradient descent) becauses look at all training sample.

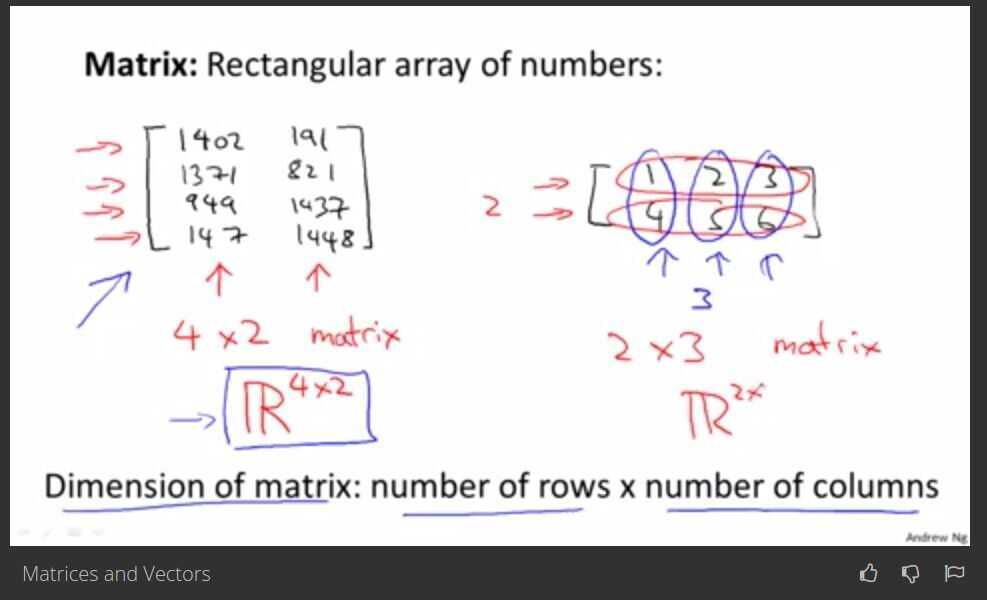
Linear Algebra Review

Matrix - Rectangular array of numbers.

Dimension of matrix : number of rows * number of columns

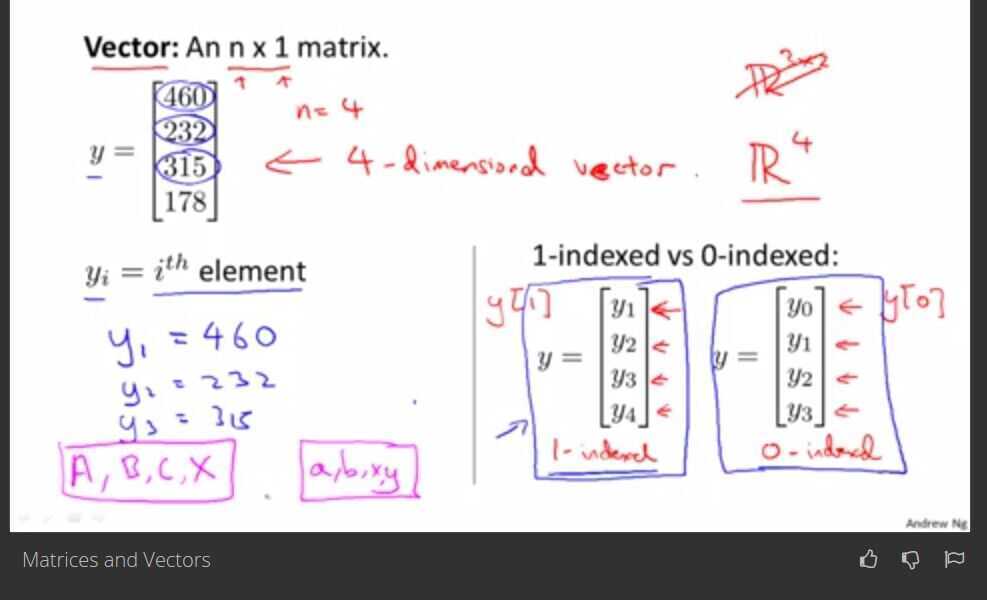
Vector - is a matrix with one column (n*1 matrix)

Uppercase for matrices

Lower case for others variables, vectors, etc.

Addition and Scalar Multiplication

Scalar multiplication is 3matrix (nmatrix).

Scalar division is ⅓ * matrix

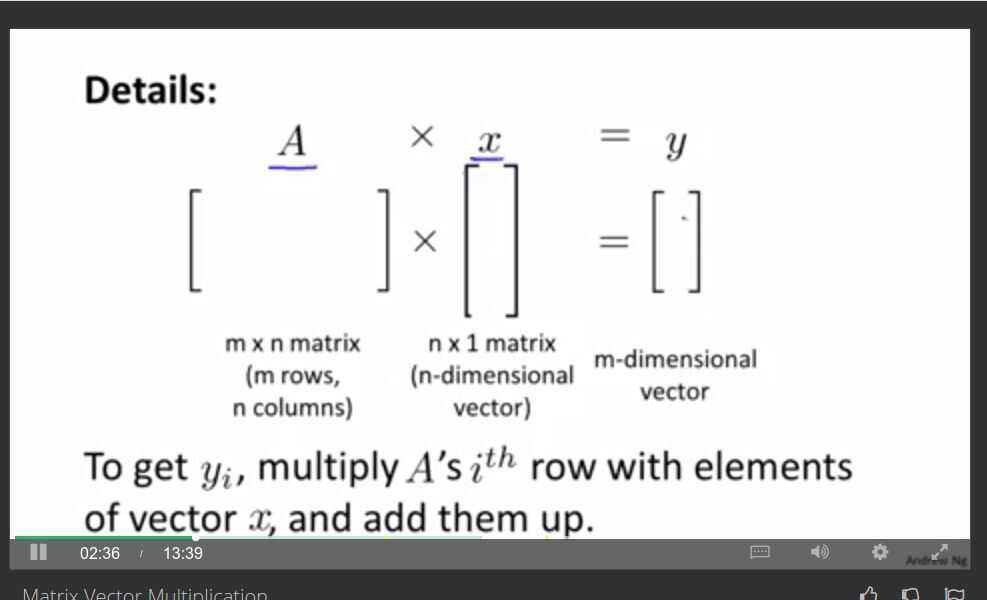
Matrix Vector Multiplication

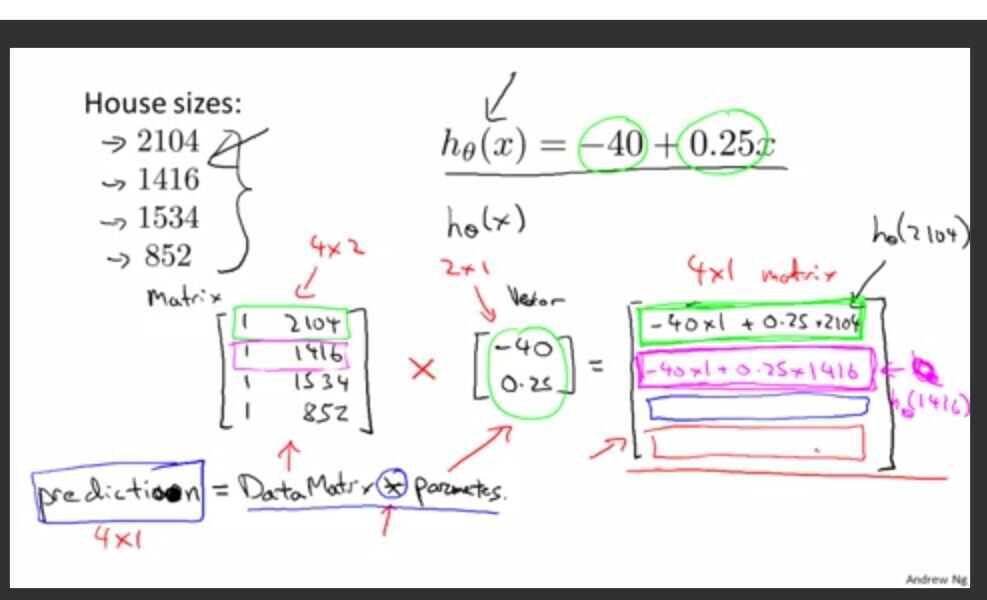
Calculating hypothesis using matrix-vector multiplication in octave its easy

Matrix - Matrix multiplication

If we have 3 hypothesis with 4 houses then,

Multiplication Properties

• Multiplication is not commutative ( AB not equal to BA)
• Multiplication is Associative ( a*(bc) = (ab)*c)
• Identity matrix (A.I = I.A = A)

Matrix Inverse and Transpose

Matrix Inverse:

• 0 does not have an inverse.
• 3 inverse is 3-1
• Matrix inverse ( A * A-1 = Identity)
• Matrix that don't have an inverse are singular or degenerate matrix
• Ex- 0 matrix doesn't have inverse.

Matrix Transpose: