Skip to main content

Binomial Random Variables

  1. Binomial Random Variables

The conditions of a binomial random variable are -

  • Made up of independent trials
  • Each trial can be classified as either success or failure
  • Fixed number of trials
  • Probability of success on each trial is constant Ex - X = Number of heads after 10 flips of a coin with P(H) = 0.6 and P(T) = 0.4

Not binomial variable - Number of kings after taking 2 cards from standard deck without replacement (It doesn't meet independent trial, the second trial depends on 1st trial) SRS - Simple Random Sample, is a sample taken so that each member in a set of n members has an equal chance of being in the sample. 2. Distributions

  • Normal distribution, (Continuous distribution - bell curve)

  • Binomial distributions (Normal distributions with discrete steps)

  • 10% rule of assuming independence between trials

  • Binomial Distribution

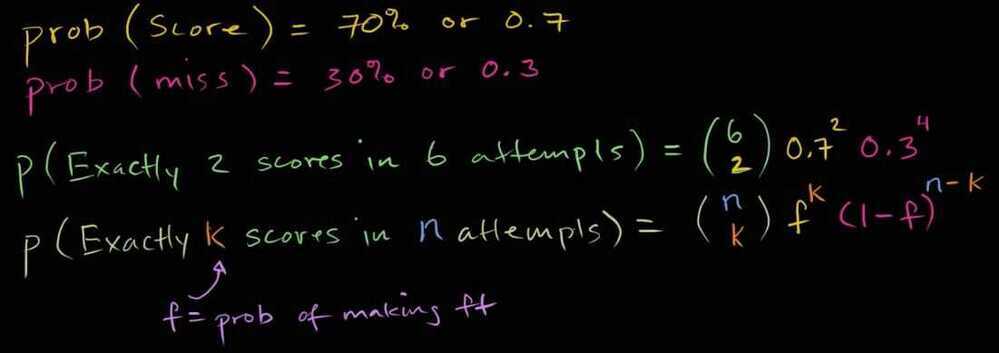
image

image

  • Binompdf (Binomial Probability Distribution Function) and Binomcdf (Binomial Cumulative Distribution Function) functions

  • Bimodal distribution

  • Uniform distribution

  • Bernoulli distribution

Others​

  • Galton Board - Every time creates normal distribution, pegs are arranged in pattern of Quincunx (pattern of 5 pegs, where 4 are on sides of square and 1 in middle, like dice - 5)
  • Follow Binomial Distribution (Central limit theorem, says that under large number of trials like 3000 balls a binomial distribution approximates a normal distribution)
  • Pascal's Triangle

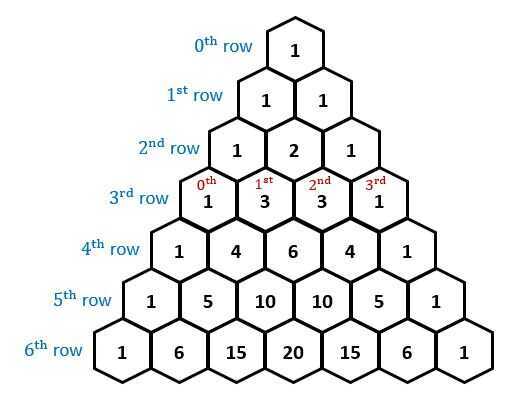
image

  • Creates Fibonacci Series

image- Rows gives sequence of coefficients in binomial powers

(a + b)^2^ = a^2^ + 2.a.b + b^2^ [FOIL - First, Outer, Inner, Last]​

(a+b)^4^ = a^4^+ 4 a^3^b + 6 a^2^b^2^+ 4 ab^3^+ b^4^

These have same coefficients as 4th row of pascal's triangle The Galton Board

References​

https://www.khanacademy.org/math/statistics-probability/random-variables-stats-library/binomial-random-variables/v/binomial-variables