Other Statistics
Gaussian Noise
Gaussian noise is statistical noise having a probability density function (PDF) equal to that of the normal distribution, which is also known as the Gaussian distribution. In other words, the values that the noise can take on are Gaussian-distributed
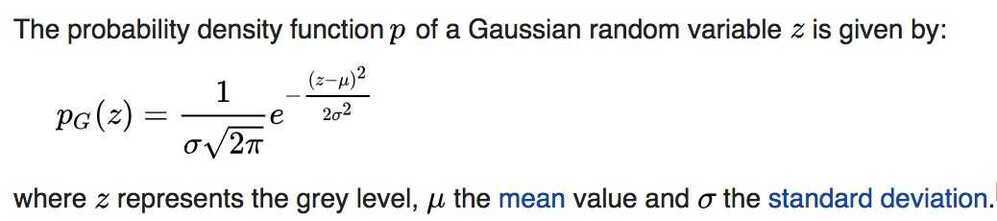
A special case is white Gaussian noise, in which the values at any pair of times are identically distributed and statistically independent (and hence uncorrelated). In communication channel testing and modelling, Gaussian noise is used as additive white noise to generate additive white Gaussian noise.
https://en.wikipedia.org/wiki/Gaussian_noise
Monotonic Function
A monotonic function is a function which is either entirely nonincreasing or nondecreasing. A function is monotonic if its first derivative (which need not be continuous) does not change sign.
Figure 1. A monotonically increasing function.
Figure 2. A monotonically decreasing function
Figure 3. A function that is not monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order.
https://en.wikipedia.org/wiki/Monotonic_function
Null Hypothesis
- (in a statistical test) the hypothesis that there is no significant difference between specified populations, any observed difference being due to sampling or experimental error.
- The idea that there's no effect
Alternative hypothesis
is one that states that sample observations are influenced by some non-random cause. From an A/B test perspective, the alternative hypothesis states that thereisa difference between the control and variant group.
F-distribution
In probability theory and statistics, the F-distribution, also known as Snedecor's F distribution or the Fisher--Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance(ANOVA), e.g., F-test.
F-test
An F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis. It is most often used when comparing statistical models that have been fitted to a data set, in order to identify the model that best fits the population from which the data were sampled. Exact "F-tests" mainly arise when the models have been fitted to the data using least squares.
F1-score
In statistical analysis of binary classification, the F1score(alsoF-score or F-measure) is a measure of a test's accuracy. It considers both the precision p and the recallrof the test to compute the score: p is the number of correct positive results divided by the number of all positive results returned by the classifier, and r is the number of correct positive results divided by the number of all relevant samples (all samples that should have been identified as positive). The F1score is the harmonic average of the precision and recall, where an F1score reaches its best value at 1 (perfect precision and recall) and worst at 0.
Matthews correlation coefficient (MCC)
The Matthews correlation coefficient (MCC) is a statistical tool that measures the quality of binary classifications:
- What it is - A statistical rate that measures the difference between predicted and actual values
- How it's used - A single-value classification metric that summarizes confusion matrices or error matrices
- What it's used for - Evaluating binary classifications, protein gamma-turn prediction, software defect prediction, and medical image analysis
- What it's better than - MCC is more reliable than accuracy and F score, which can produce misleading results on imbalanced datasets
- How it's calculated - MCC returns values between −1 and +1, with +1 representing a perfect prediction, 0 representing no better than random prediction, and −1 indicating total disagreement between prediction and observation
Moving Average (MA)
In statistics, a moving average(rolling average or running average) is a calculation to analyze data points by creating series of averages of different subsets of the full data set. It is also called a moving mean (MM) or rolling mean and is a type of finite impulse response filter.
Given a series of numbers and a fixed subset size, the first element of the moving average is obtained by taking the average of the initial fixed subset of the number series. Then the subset is modified by "shifting forward"; that is, excluding the first number of the series and including the next value in the subset.
A moving average is commonly used with time series data to smooth out short-term fluctuations and highlight longer-term trends or cycles. The threshold between short-term and long-term depends on the application, and the parameters of the moving average will be set accordingly. For example, it is often used in technical analysis of financial data, like stock prices, returns or trading volumes. It is also used in economics to examine gross domestic product, employment or other macroeconomic time series. Mathematically, a moving average is a type of convolution and so it can be viewed as an example of a low-pass filter used in signal processing. When used with non-time series data, a moving average filters higher frequency components without any specific connection to time, although typically some kind of ordering is implied. Viewed simplistically it can be regarded as smoothing the data.- Simple Moving Average
- Cumulative Moving Average
- Weighted Moving Average
- Exponential Moving Average
- Centered Moving Average
https://en.wikipedia.org/wiki/Moving_average
Parameter Space
In statistics, aparameter space is the space of all possible combinations of values for all the different parameters contained in a particular mathematical model. The ranges of values of the parameters may form the axes of a plot, and particular outcomes of the model may be plotted against these axes to illustrate how different regions of the parameter space produce different types of behaviour in the model.
https://en.wikipedia.org/wiki/Parameter_space
Ziph's Law
Zipf's law(/zɪf/) is an empirical law formulated using mathematical statistics that refers to the fact that many types of data studied in the physical and social sciences can be approximated with a Zipfian distribution, one of a family of related discrete power lawprobability distributions.Zipf distributionis related to the zeta distribution, but is not identical.
For example, Zipf's law states that given some corpus of natural language utterances, the frequency of any word is inversely proportional to its rank in the frequency table. Thus the most frequent word will occur approximately twice as often as the second most frequent word, three times as often as the third most frequent word, etc.: the rank-frequency distribution is an inverse relation. For example, in the Brown Corpus of American English text, the word the is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's Law, the second-place wordofaccounts for slightly over 3.5% of words (36,411 occurrences), followed byand(28,852). Only 135 vocabulary items are needed to account for half the Brown Corpus.
https://en.wikipedia.org/wiki/Zipf%27s_law
Power Law Distribution
In statistics, apower law is a functional relationship between two quantities, where a relative change in one quantity results in a proportional relative change in the other quantity, independent of the initial size of those quantities: one quantity varies as a power of another. For instance, considering the area of a square in terms of the length of its side, if the length is doubled, the area is multiplied by a factor of four.
An example power-law graph, being used to demonstrate ranking of popularity. To the right is the long tail, and to the left are the few that dominate (also known as the 80--20 rule).
https://en.wikipedia.org/wiki/Power_law
Pivot Table
A pivot table is a table of statistics that summarizes the data of more extensive table (such as from a database, spreadsheet, or business intelligence program). This summary might include sums, averages, or other statistics, which the pivot table groups together in a meaningful way.
Pivot tables are a technique in data processing. They enable a person to arrange and rearrange (or "pivot") statistics in order to draw attention to useful information.
https://en.wikipedia.org/wiki/Pivot_table
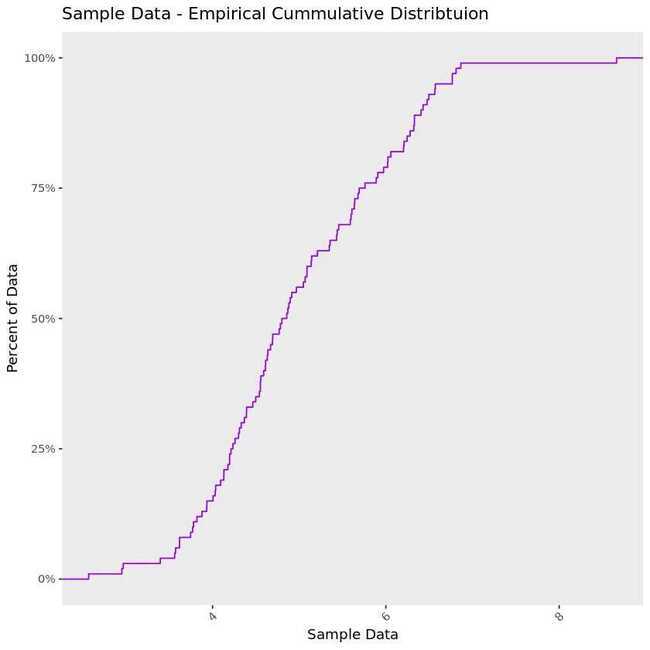
Empirical Cumulative Distribution Function
This plot draws a line showing us what percent of our data falls below a certain value on the x-axis. Here the x-axis displays the value of the data and the y-axis the percent of our data that falls below a specific value on the x-axis. On the chart below, take the point 6 on the x-axis and use your finger to trace a straight path up until you hit the line - the value on the y-axis at the point you hit the line is about 75%. So 75% of the data in the example below are lower than 6.
Rank Order Scale / Rank Ordering / Ranking scale
Rank order items are analyzed using Spearman or Kendall correlation.
Statistical Power
https://machinelearningmastery.com/statistical-power-and-power-analysis-in-python
Effect Size
https://machinelearningmastery.com/effect-size-measures-in-python