Vectors and Spaces
Vectors
- Vector = Magnitude + Direction
Ex - 5mph is a scaler quantity, because it doesn't tell the direction in which object is moving.
Ex - 5mph East is a vector quantity (and we will not call this as speed, we will call this as velocity, therefore velocity is a vector quantity)

-
Real Coordinate Space - Can be any dimensions, all possible real-valued ordered 2-tuple for a 2 dimensional real coordinate space.
-
Adding Vectors algebraically and graphically
-
Multiplying vector by a scaler ( change its magnitude, but scale it only on the same dimension, colinear )
-
Unit Vectors
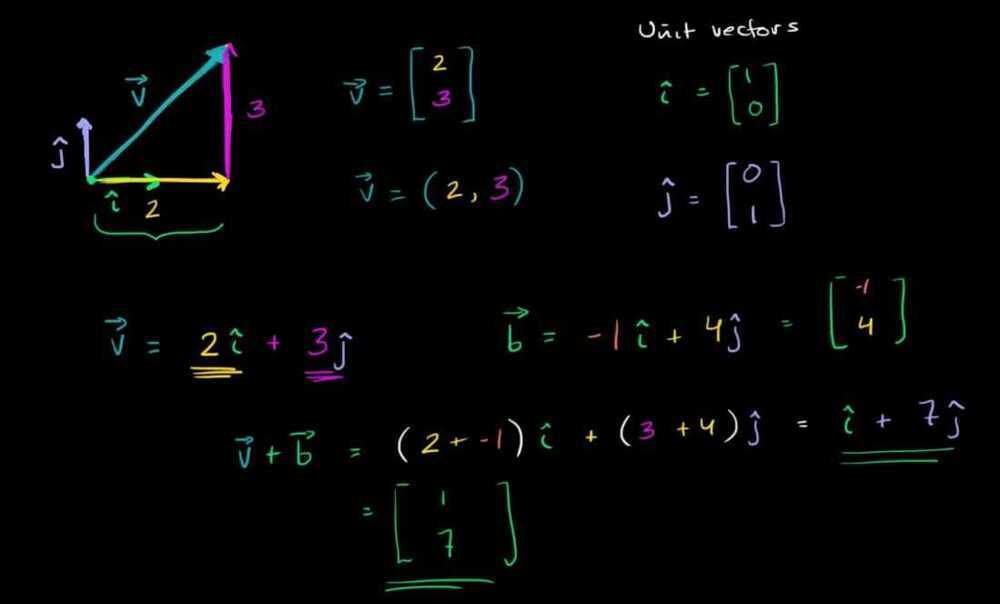
- Parametric representations of the line
Linear combinations and spans
span(v1 + v2 + v3 + ... + vn) = {c1v1 + c2v2 + c3v3 + ... + cnvn | ci belongs to set of Real numbers and 1 <= i <= n}
Linear dependence and independence
-
Linear dependent - Means one vector in the set can be represented as other vectors in the set.
-
Linear Independent - If we cannot scale using any scalar one vector to the other vector in the set, than both are linearly independent of each other
C1 and C2 must be equal to 0 for R2
Subspaces and the basis for a subspace
- Must contain 0 vector
- Closure under scalar Multiplication - In order to be in a subspace, any vector multiplied by a real scalar must also be in the subspace
- Closure under Addition - If we add two vectors belonging to the same subspace, than the addition of both the vectors must also belong to the same subspace.
- Span of n vectors is a valid subspace of Rn
- S is a basis of V, if something is a basis for a set, that means that, if you take the span of those vectors, you can get to any of the vectors in that subspace and that those vectors are linearly independent.
- Span (s) = R2
- Must be Linearly Independent
- Standard Basis =
T = {[1 0] , [0 1]}
Vector dot and cross products
- Dot product
- Vector dot product is commutative, V.W = W.V
- Vector dot product is distributive, (V + W).X = (V.X + W.X)
- Vector dot product is associative ( (c.V).W = c.(V.W) )
- Length of vector X = ||X||
||X||^2^ = X.X- Cauchy -Schwarz inequality
- |X.Y|<= ||X||.||Y||
- |X.Y| = ||X||.||Y|| only when X and Y are colinear i.e. X = c.Y
- Vector Triangle Inequality
- Angles between Vectors
- (A.B) = ||A||*||B||*cos Θ
- If A and B are perpendicular than there dot product is 0, since cos 90 = 0
- If A.B = 0 (dot product of vector A and dot product of vector B is equal to 0) and A and B are non zero vectors than A and B are perpendicular to each other.
- But if only A.B = 0 satisfies, than A and B are orthogonal
- All perpendicular vectors are Orthogonal
- Zero vector is orthogonal to everything else, even to itself
Matrices for solving systems by elimination
Null space and column space
References
https://www.khanacademy.org/math/linear-algebra/vectors-and-spaces