3Blue1Brown

1. Vectors
2. Linear combinations, span and basis vectors
3. Linear transformations and matrices
4. Matrix multiplication as composition
5. Three dimensional linear transformation
6. The determinant
7. Inverse matrices, column space, rank and null space
8. Non square matrices
9. Dot product and duality
10. Cross product
11. Cross product in the light of linear transformations
12. Change of basis
13. Eigenvectors and eigenvalues
14. Abstract vector spaces

Vectors

• Vector addition (adding two vectors)
• Scalar multiplication (increasing the length of a vector by a given number)

Linear combinations, span and basis vectors

called as i hat and j hat

Linearly dependent vectors - If one vector can be removed without changing the span of the vectors. i.e. one of the vectors can be expressed as a linear combination of the other vector

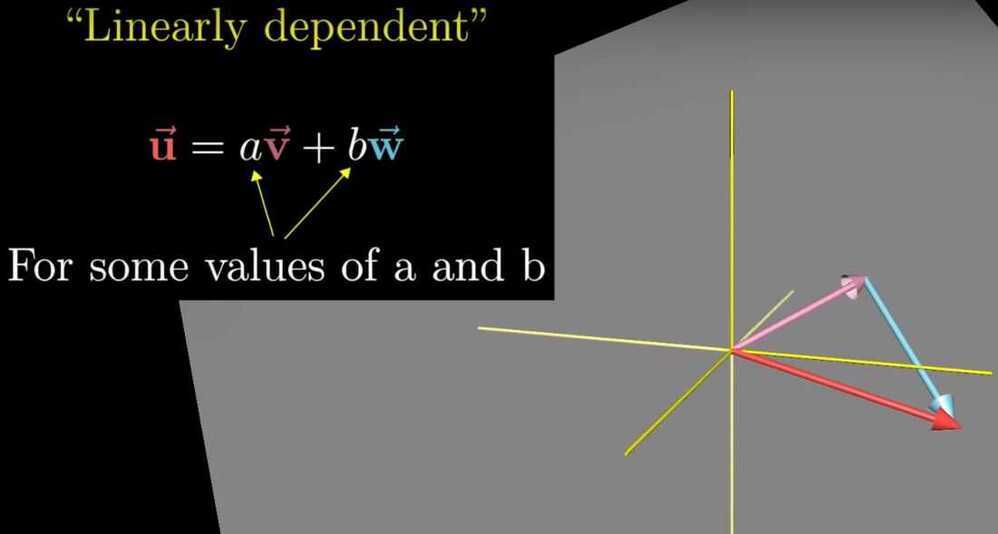
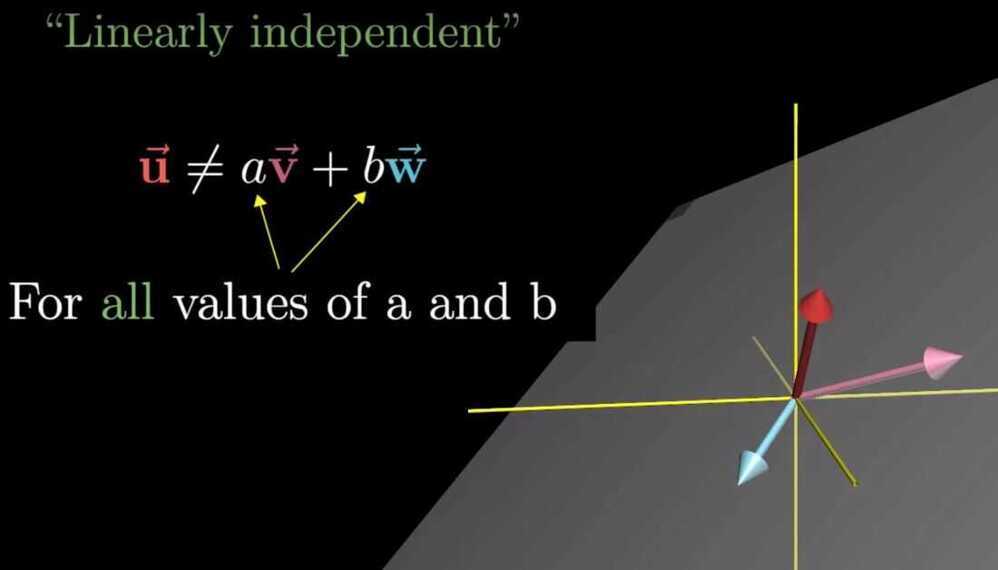
Basis - The basis of a vector space is a set of linearly independent vectors that span the full space

Linear Transformations and Matrices

For transformations to be linear, there are two property

• All lines must remain line and not get curved
• Origin must remain fixed in place

Grid lines remain parallel and evenly spaced

Matrix Multiplication as composition

If you apply a rotation transformation followed by a shear transformation, the combined effect is a composition of both rotation and shear transformation

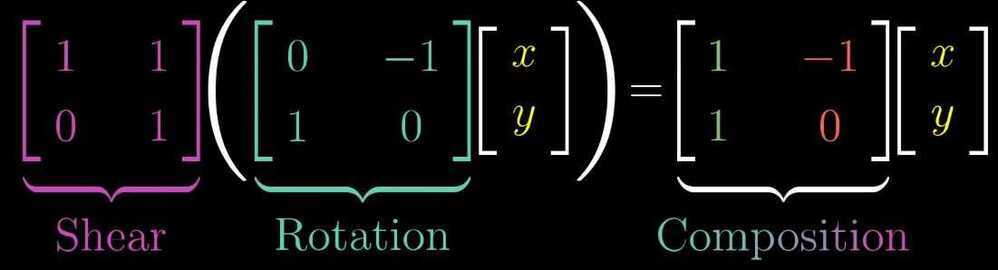
In matrix multiplication, order matters

But Matrix multiplication is associative i.e. (AB)C = A(BC)

Three dimensional linear transformations

The determinant

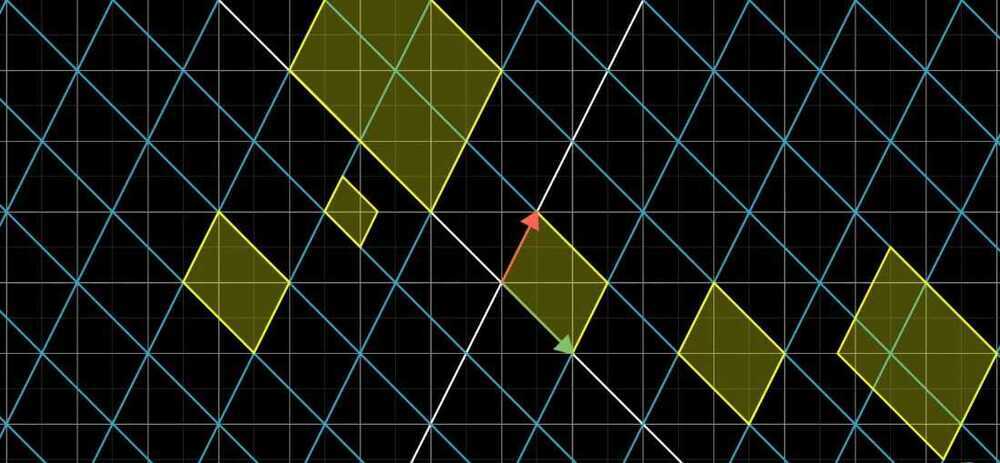
• If one area changes by some factor than every area changes by that factor.
• The determinant of a transformation is the change in area of a grid after applying linear transformation
• The factor by which a linear transformation changes any area is called the determinant of that transformation.
• Negative determinant tells that orientation of space is inverted.
• In 3 dimensions, determinant tells us how much volume gets scaled.

Volume of the parallelepiped

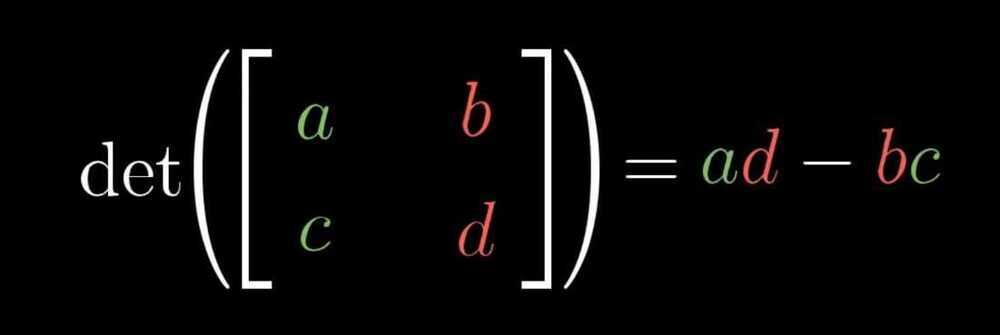
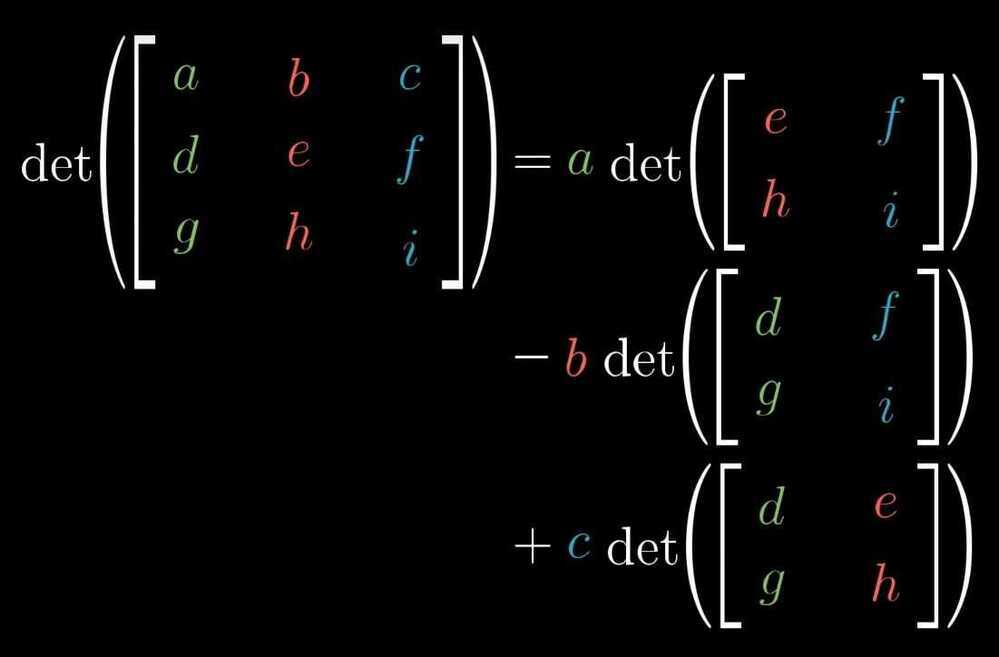
Inverse matrices, column space, rank and null space

• Gaussian Elimination
• Row echelon form
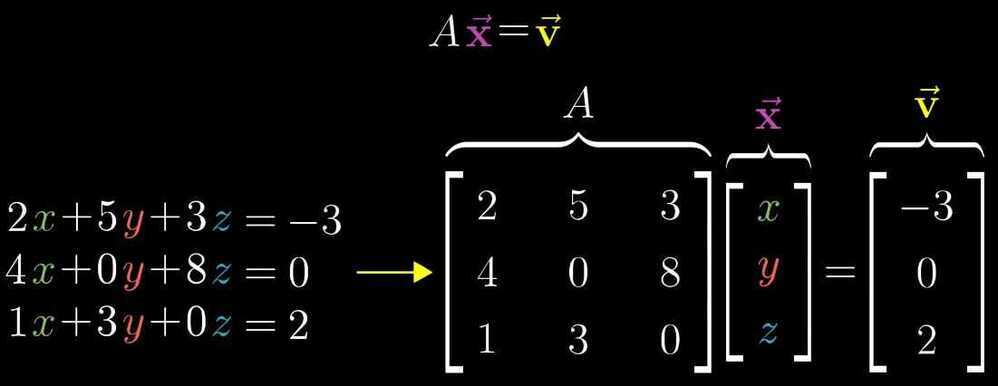
• Linear system of equations

- Inverse Transformation

A^-1^ A = [[1 0] [0 1]] Identity Transformation (changes nothing)

Until det(A) not equal to 0, A^-1^ exists - Rank - Number of dimensions in the output

• Rank 1 - One dimensional line

• Rank 2 - Two dimensional plane

• Rank 3 - Three dimensional 3d space

• Set of all possible outputs of the matrix is called the "column space" of the matrix A

• Full rank - When this rank is as high as it can be meaning it equals the number of column, we call the matrix full rank

• Null Space Kernel - All the vectors that squishes into origin when transformation takes place

In Ax = v, when v happens to be the zero vector, null space gives all of the possible solution to the linear equation

Non Square Matrices as transformations between dimensions

• A 2x3 matrix i.e. there are 2 rows and 3 columns represent that the transformation starts in 3 dimension and the landing space is represented in 2 dimension

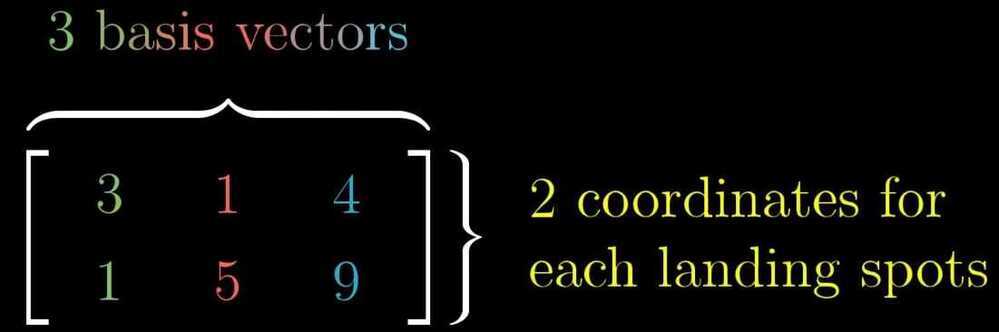
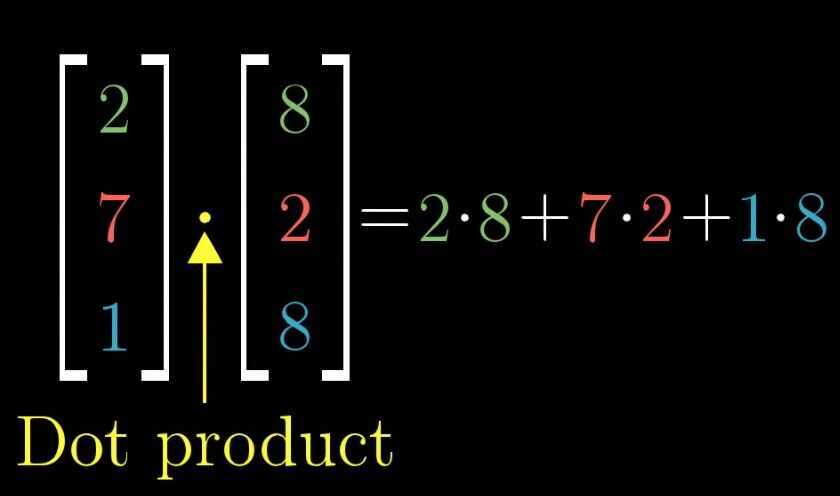
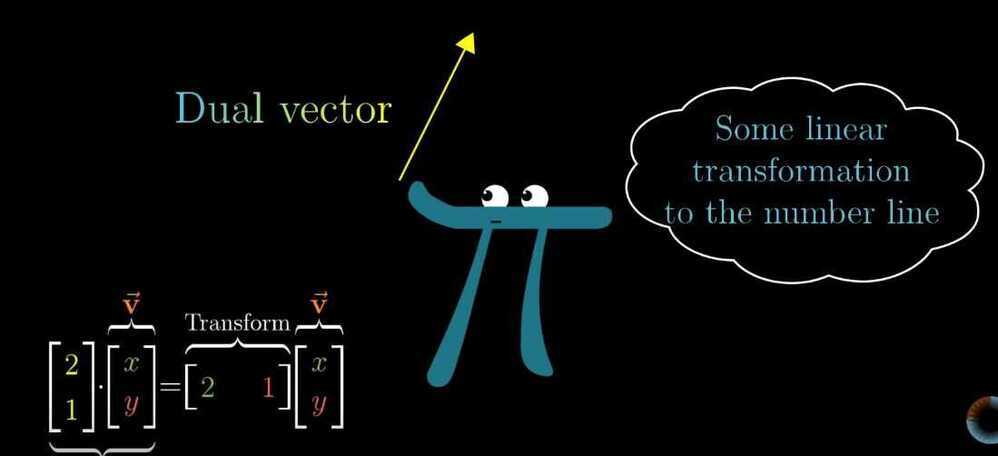
Dot products and duality

Matching coordinates, multiplying pair and adding them together.

If we projected vector w onto the line that passes through the origin and the tip of vector v, multiplying the length of this projection, by the length of v, we have the dot product.

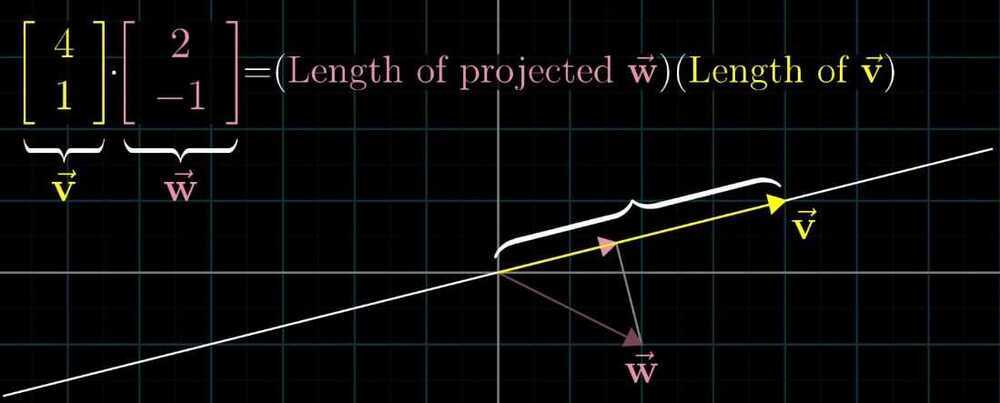
- If vectors are pointing in the same direction, then the dot product is positive

• If vectors are perpendicular to each other, there dot product is 0
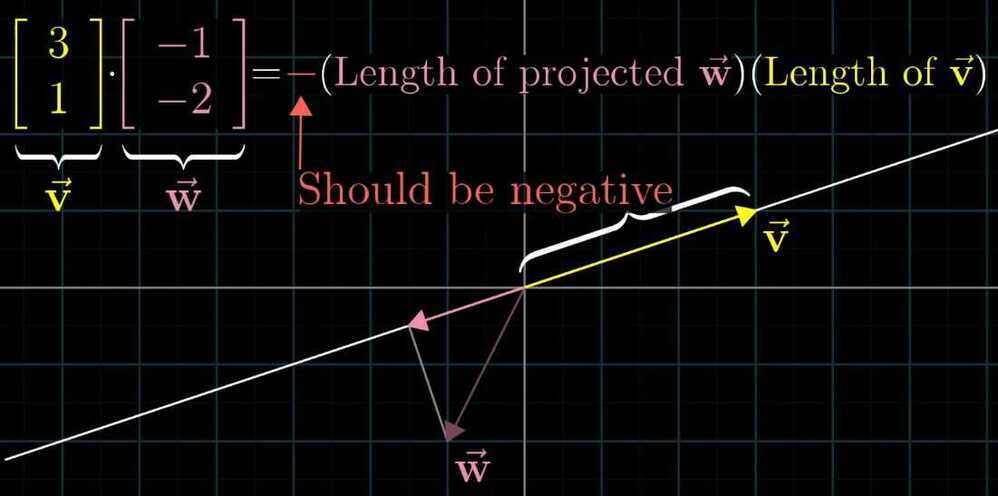
• If vectors are pointing in the opposing direction, then there dot product is negative
• Order doesn't matter, V.W = W.V
• Dot product is a very useful geometric tool for understanding projections, and for testing whether or not vectors tend to point in the same direction

Cross Products

If v is to the right of w, than cross product is positive

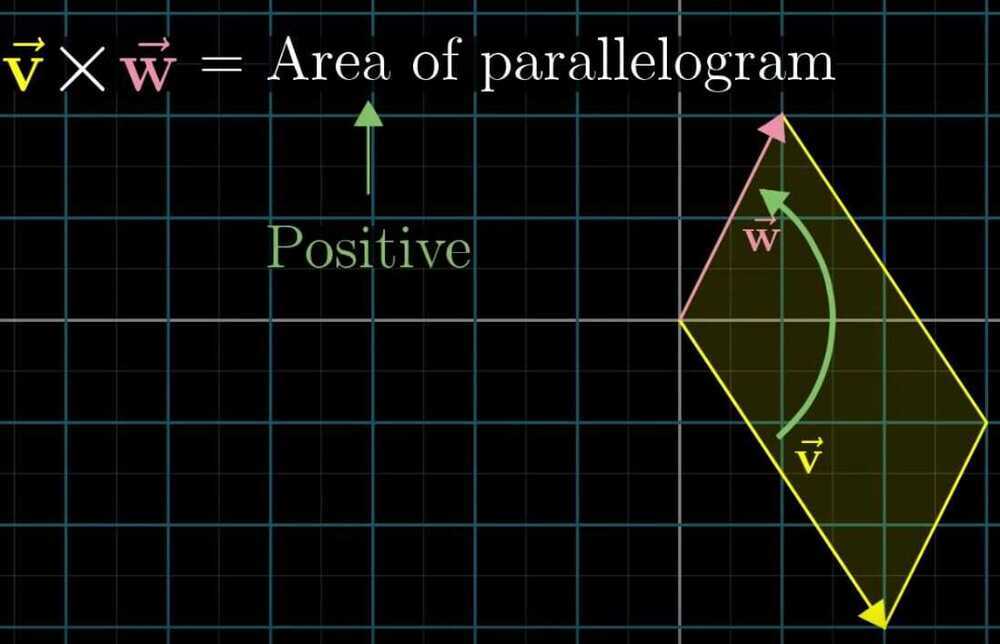
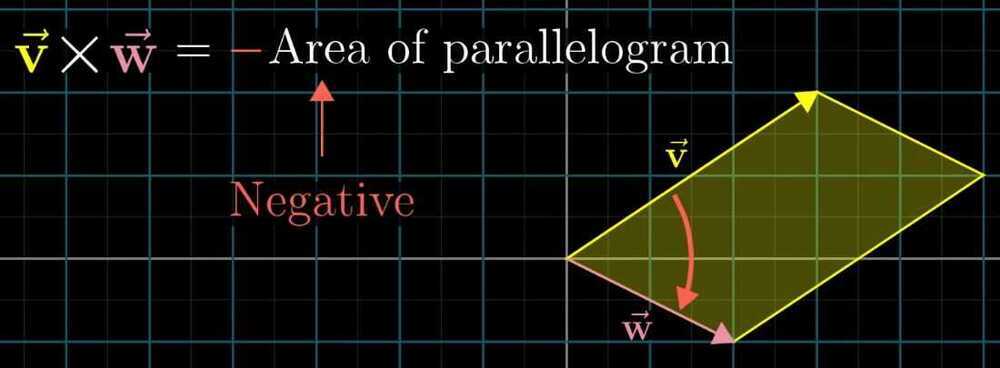
If v is to the left of w, than cross product is negative

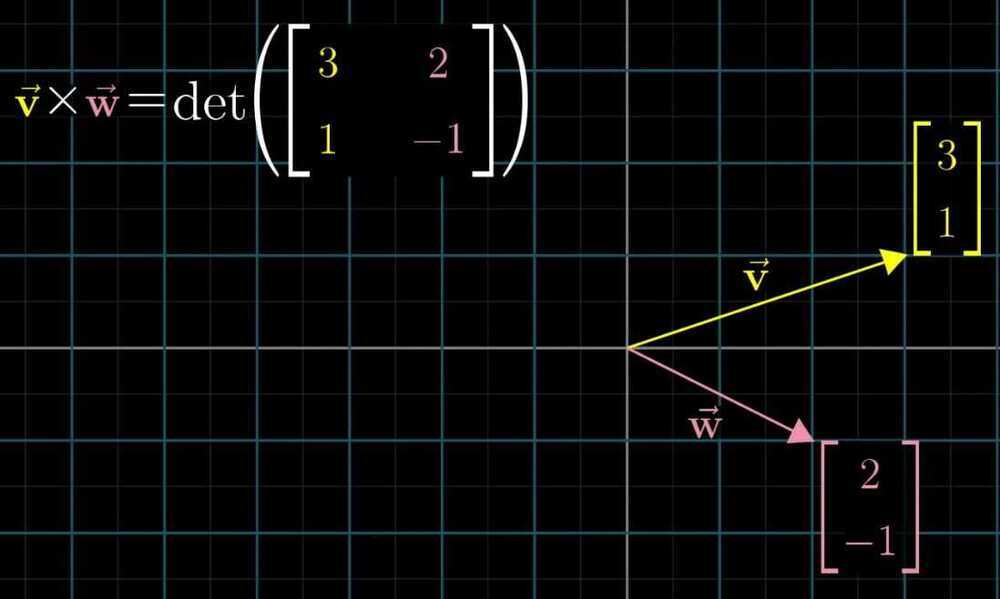- Cross product of two perpendicular vectors are greater than the vectors that are pointing in very similar direction

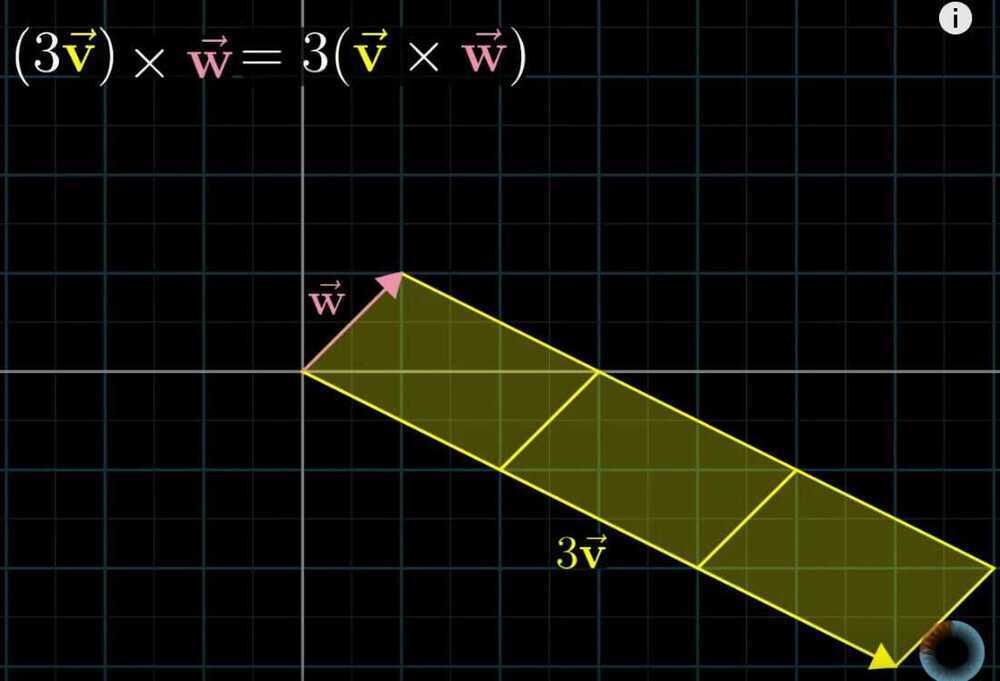
• If we scale a vector by a factor of a, than area of parallelogram also scales up by a factor of a

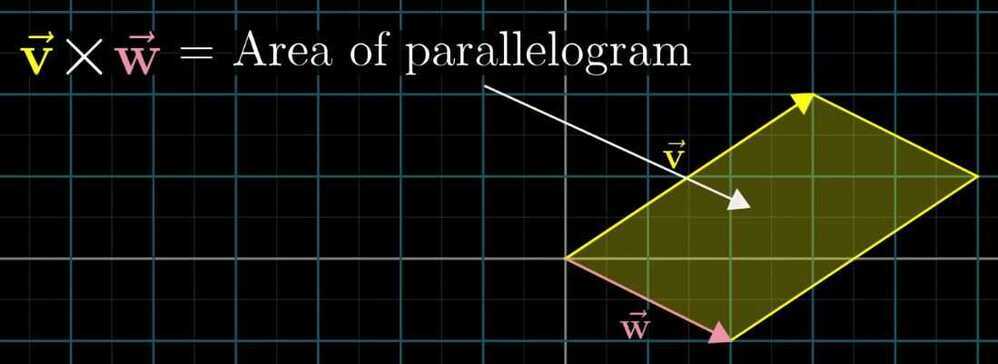
Cross product of two vectors is a vector that is the area of the parallelogram and is perpendicular to the parallelogram and in the direction of the thumb of the right hand rule.

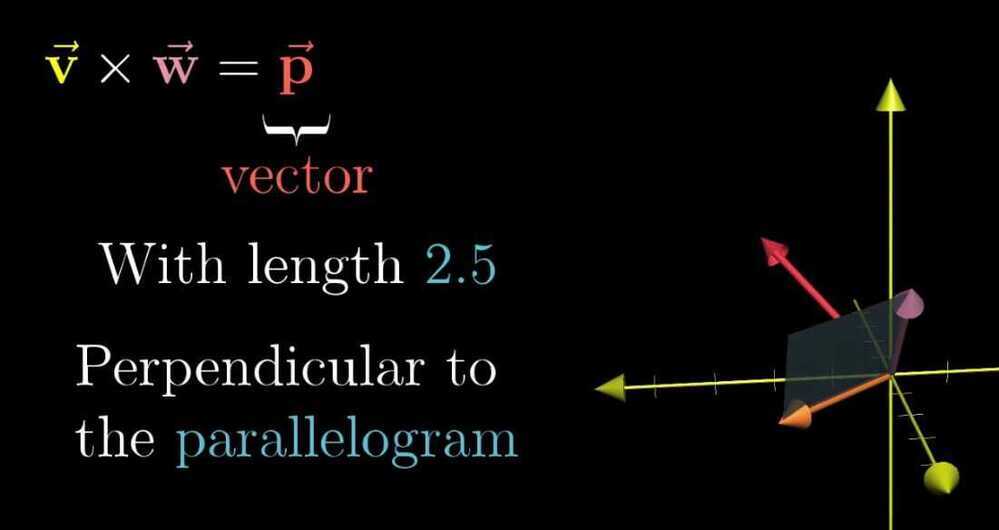
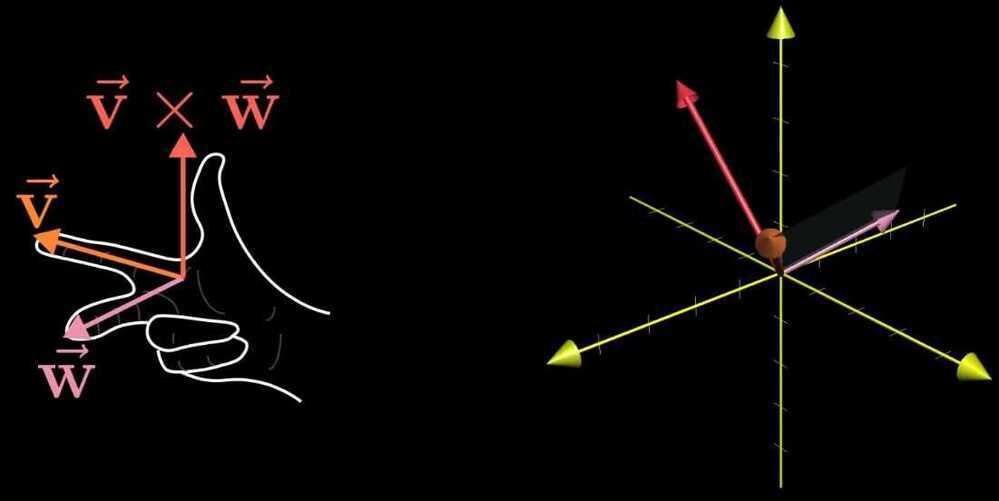
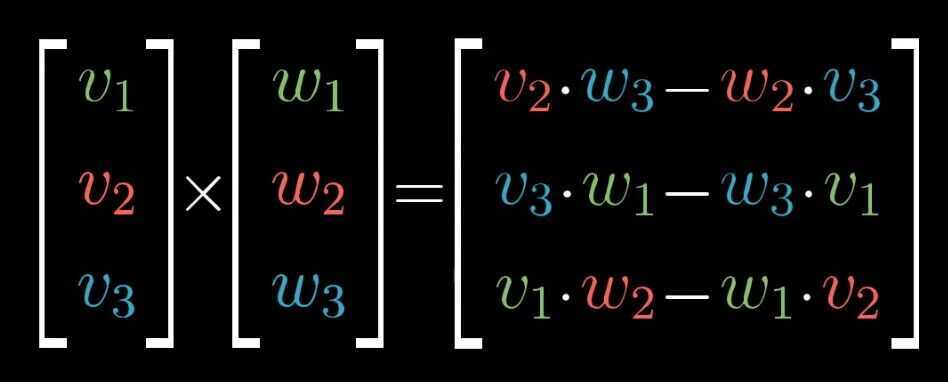
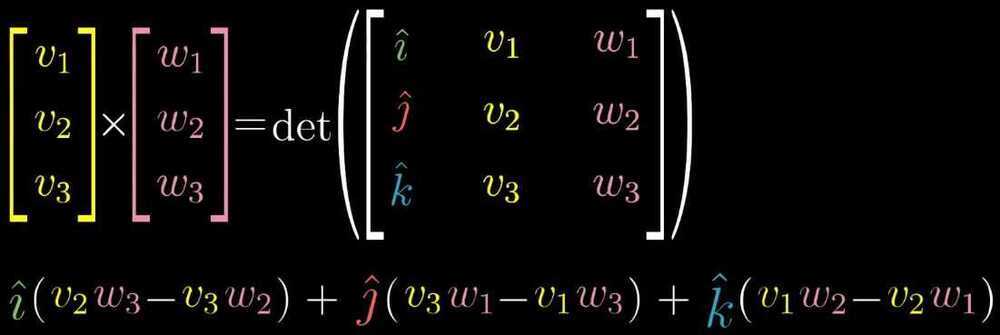
Cross Product in the light of linear transformations

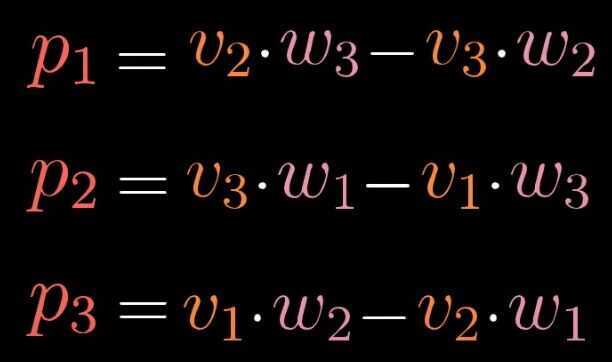
Change of basis

• Coordinate system
• Alternate coordinate system
• How do you translate between coordinate systems
• Matrix multiplication by "Inverse change of basis matrix"
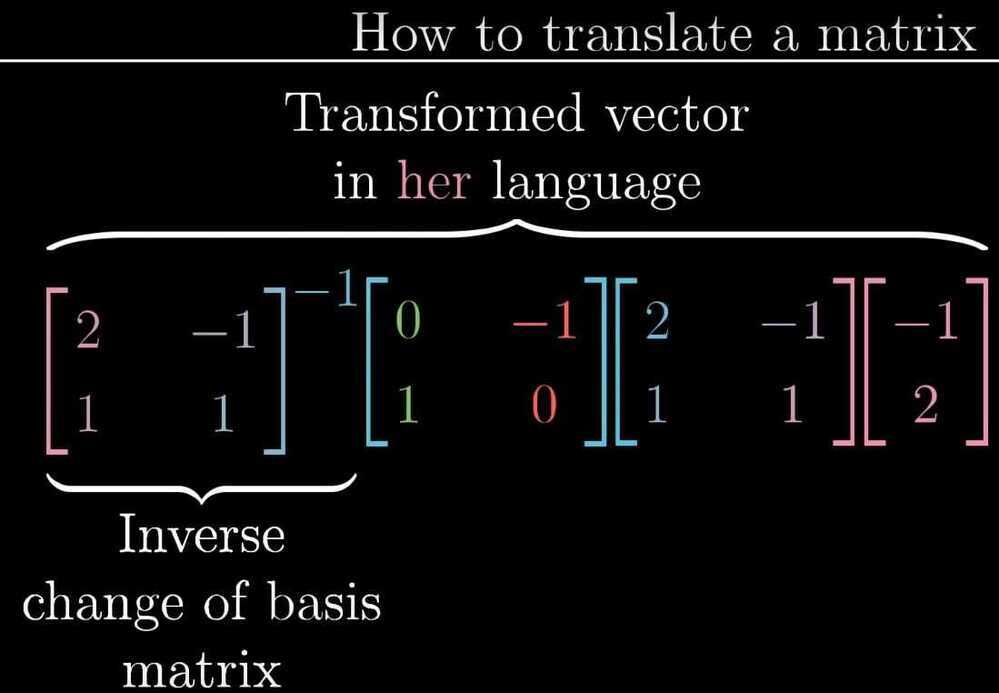
• How to translate a matrix
  • Start with any vectors written in Jennifer's language
  • Translate it to our language using change of basis matrix
  • Apply transformation matrix in our language, this tells us where that vector lands but still in our language
  • Apply the inverse change of basis matrix to get the transformed vector but in Jennifer's language

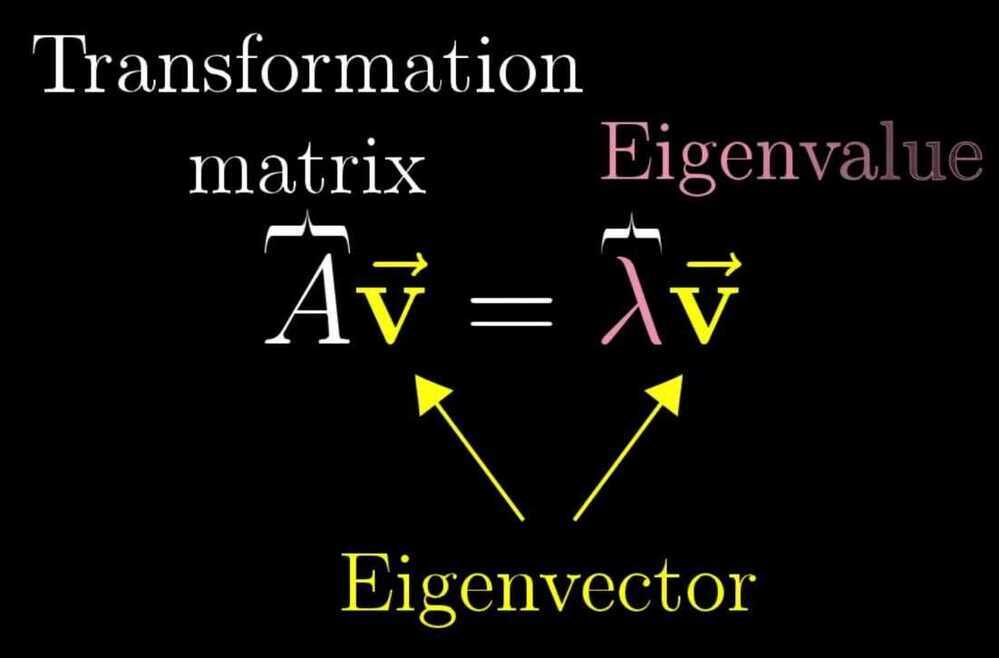
Eigenvectors and eigenvalues

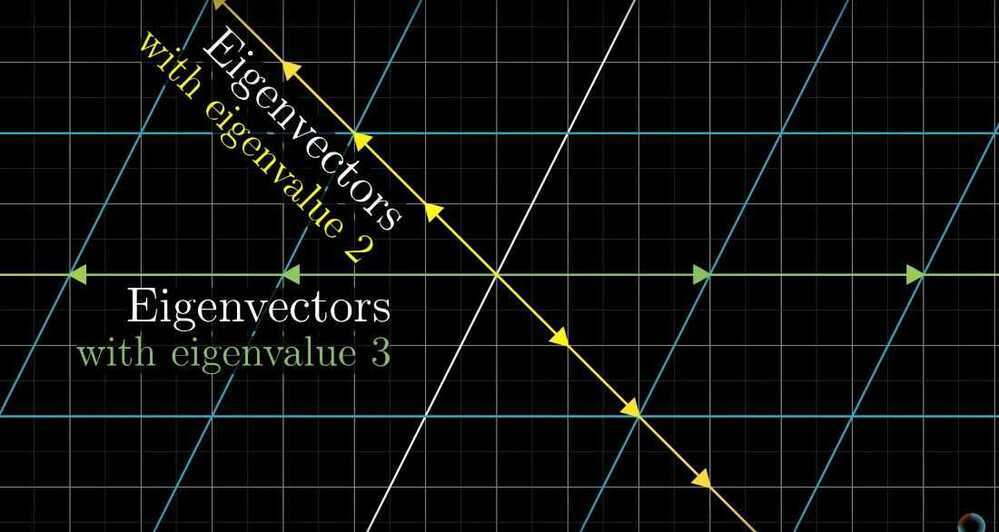
Eigenvectors - the vectors that doesn't change its span after a transformation. The factor by which they are changed (either stretched or squished) during the transformation is eigenvalue.

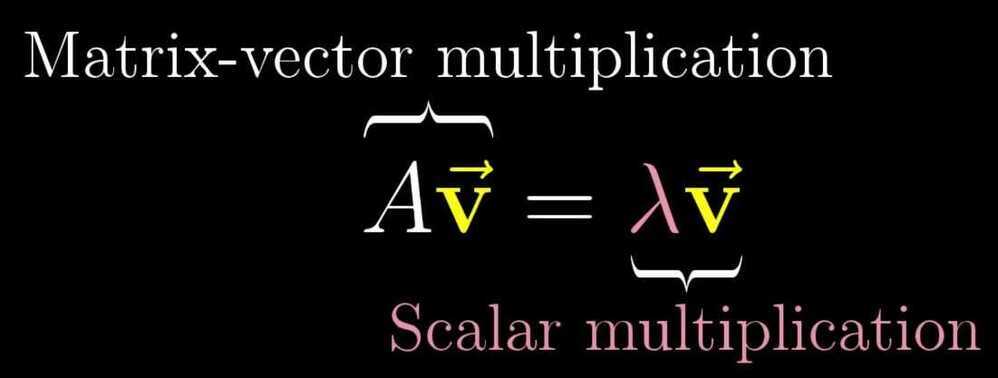- Negative eigenvalue corresponds to flipping during transformation

• There could be no eigenvectors in a transformation

Ex - Rotation by 90 degrees

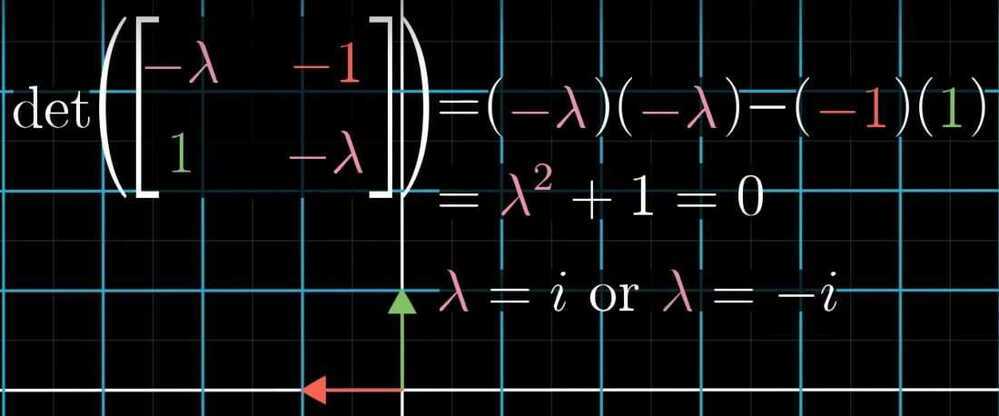
Since there are no real numbers, therefore there are no eigenvectors for this transformation- A transformation can have a single eigenvalue with a lot of eigenvector

Ex - Scaling by some scalar eg. 2, there is only one eigenvalue of 2, but all the vectors have that value.- Diagonal matrix - all values other than diagonal is 0

All the basis vectors are eigenvectors, with the diagonal entries of this matrix being there eigenvalues- Eigenbasis

We can change our coordinate system so that our eigenvectors are our basis vectors

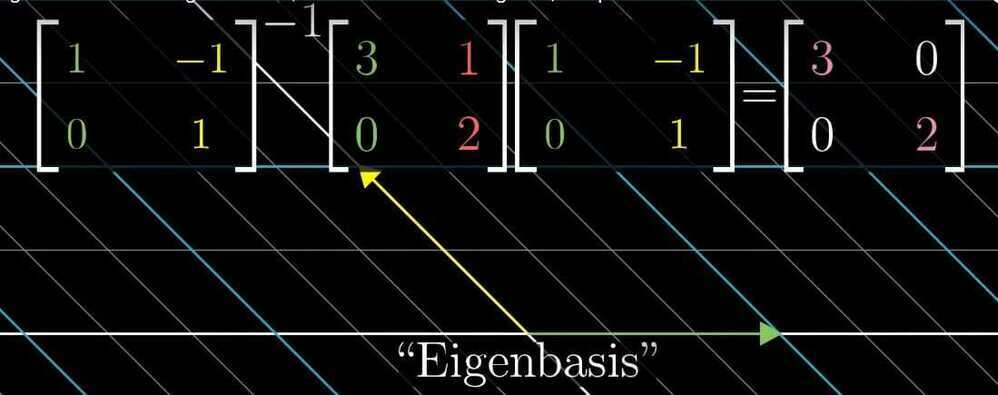
Abstract Vector Spaces

- Additivity - If you add two vectors and then perform a transformation, the result is same vector for the transformed addition of vectors and the previous addition vector.

• Scaling - Is if you scale a vector v by some number, then apply the transformation, you get the same ultimate vector as if you scale the transformed version of v by that same amount.
• Linear transformations preserve addition and scalar multiplication

References

Essence of linear algebra