Suffix Tree
In computer science, a suffix tree (also called PAT tree or, in an earlier form, position tree) is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.
The construction of such a tree for the string S takes time and space linear in the length of S. Once constructed, several operations can be performed quickly, for instance locating a substring in S, locating a substring if a certain number of mistakes are allowed, locating matches for a regular expression pattern etc. Suffix trees also provide one of the first linear-time solutions for the longest common substring problem. These speedups come at a cost: storing a string's suffix tree typically requires significantly more space than storing the string itself.
The suffix tree for the string S of length n is defined as a tree such that:
- The tree has exactly n leaves numbered from 1 to n.
- Except for the root, every internal node has at least two children.
- Each edge is labelled with a non-empty substring of S.
- No two edges starting out of a node can have string-labels beginning with the same character.
- The string obtained by concatenating all the string-labels found on the path from the root to leaf i spells out suffix S [i..n], for i from 1 to n.
Since such a tree does not exist for all strings, S is padded with a terminal symbol not seen in the string (usually denoted $). This ensures that no suffix is a prefix of another, and that there will be n leaf nodes, one for each of the n suffixes of S. Since all internal non-root nodes are branching, there can be at most n− 1 such nodes, and n+(n−1)+1=2n nodes in total (n leaves, n−1 internal non-root nodes, 1 root).
Generalized Suffix Tree
A generalized suffix tree is a suffix tree made for a set of words instead of a single word. It represents all suffixes from this set of words. Each word must be terminated by a different termination symbol or word.
How to build a Suffix Tree for a given text?
As discussed above, Suffix Tree is compressed trie of all suffixes, so following are very abstract steps to build a suffix tree from given text.
- Generate all suffixes of given text.
- Consider all suffixes as individual words and build a compressed trie.
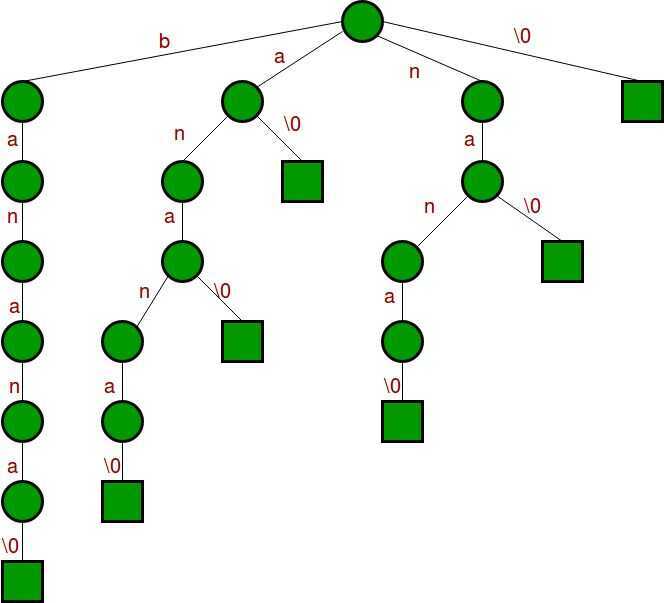
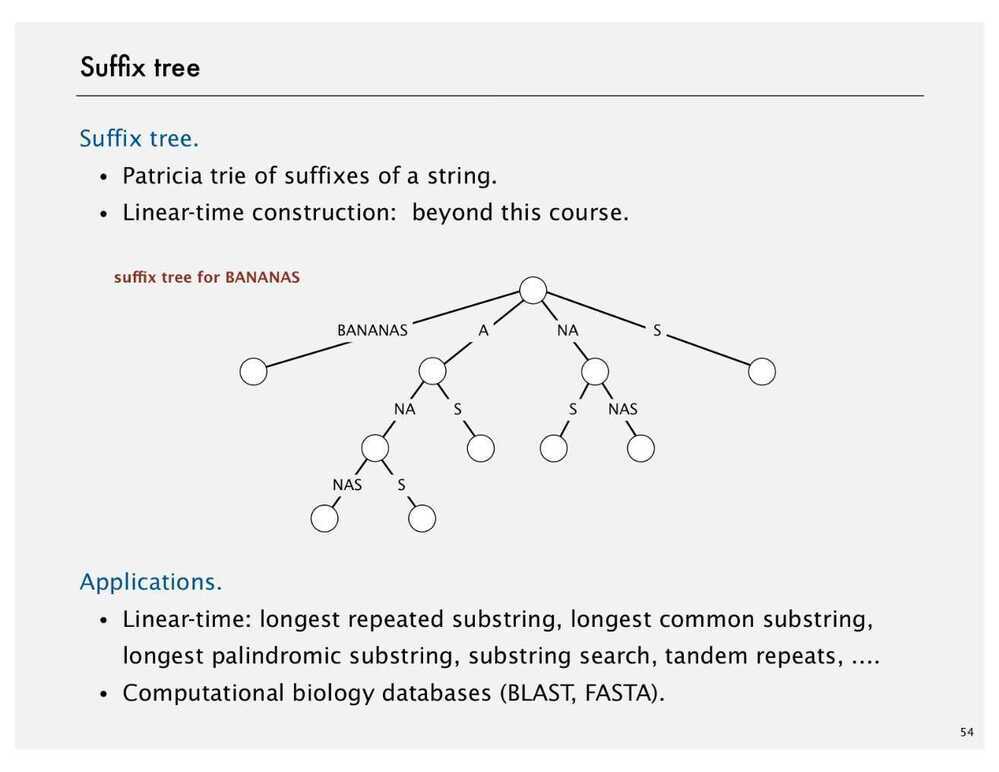
Let us consider an example text "banana0" where '0' is string termination character. Following are all suffixes of "banana0"
banana0 anana0 nana0 ana0 na0 a0 0
If we consider all of the above suffixes as individual words and build a trie, we get following.
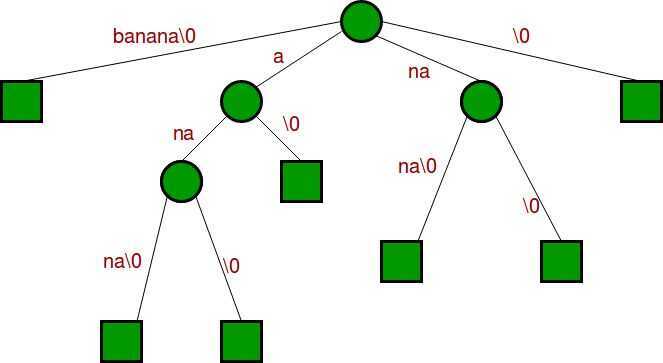
If we join chains of single nodes, we get the following compressed trie, which is the Suffix Tree for given text "banana0"
Suffix Tree and Its Construction
Suffix Tree were first introduced to solve SubString Problem -
The substring problem: Pre-process text T so that the computation string matching problem is solved in time proportional to m, the length of pattern P.
Use Case - Performing intensive queries on a big database, which is represented by T. Once the suffix tree for T is built each query is proportional to O(m) time.
Problems
- SME - String Matching Existence problem - Given a pattern P and a text T, determine whether there is an occurance of P in T.
- SMC - String Matching Computation problem - Given a pattern P and a text T, determine all the occurance of P in T
Advanced
- Ukkonen's Linear Time Algorithm
- Implicit's Suffix Tree
An implicit suffix tree for a string S is a tree obtained from T(S$) by performing the following operations:
- Remove all the terminal symbols $.
- From the resulting tree, remove all edges without label.
- Finally, from the resulting tree, remove all nodes that do not have at least two children.
- Suffix Links
- Extension Algorithm
- Edge Label Compression
- Phase Algorithm