2-3 Search Trees
Properties
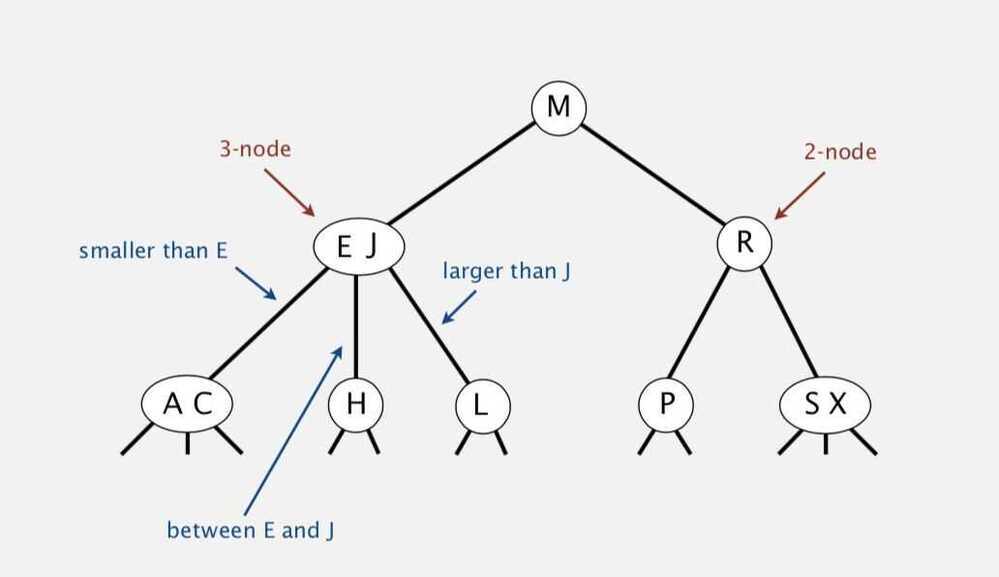
- Every non-leaf is a 2-node or a 3-node. A 2-node contains one data item and has two children. A 3-node contains two data items and has 3 children.
- All leaves are at the same level (the bottom level)
- All data is kept in sorted order
- Every non-leaf node will contain 1 or 2 fields.2-3 Tree
Allow 1 or 2 keys per node -
- 2-node: one key, two children
- 3-node: two keys, three children
Symmetric order: Inorder traversal yields keys in ascending order
Perfect balance: Every path from root to null links has same length
Each transformation maintains symmetric order and perfect balance
Search
・Compare search key against keys in node. ・Find interval containing search key. ・Follow associated link (recursively).
Insertion into a 3-node at bottom
・Add new key to 3-node to create temporary 4-node. ・Move middle key in 4-node into parent. ・Repeat up the tree, as necessary. ・If you reach the root and it's a 4-node, split it into three 2-nodes.
Height of a 2-3 tree increases only when root node of the tree splits
Tree height
・Worst case: lg N. [all 2-nodes] ・Best case: log3 N ≈ .631 lg N. [all 3-nodes] ・Between 12 and 20 for a million nodes. ・Between 18 and 30 for a billion nodes.
Guaranteed logarithmic performance for search and insert
Direct implementation is complicated, because
・Maintaining multiple node types is cumbersome ・Need multiple compares to move down tree ・Need to move back up the tree to split 4-nodes ・Large number of cases for splitting