MO's Algorithm
Query Square Root Decomposition
-
Range Query
-
Point Update
-
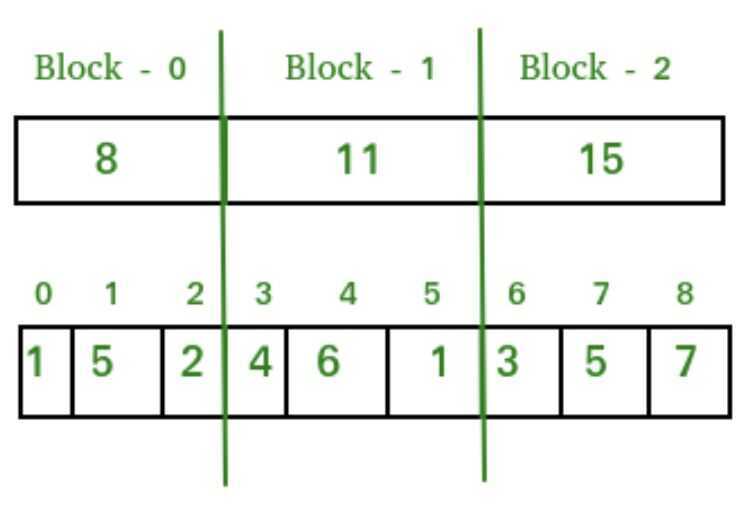
Divide the array in sqrt(n) blocks, maintain sum or prefix-sum of each block
- Any range query can be efficiently calculated by summing all sqrt(n) blocks or part of some blocks
- Any point update can be done by altering only the sum of that block only
Problem - We are given an array and a set of query ranges, we are required to find sum of every query range
Naive - ANaive Solution is to run a loop from L to R and calculate sum of elements in given range for every query [L, R]
Time Complexity - O(m*n)
The idea ofMO's algorithmis to pre-process all queries so that result of one query can be used in next query. Below are steps.
Let**a[0...n-1]be input array andq[0..m-1]**be array of queries.
-
Sort all queries in a way that queries with L values from 0 to √n -- 1 are put together, then all queries from √n to 2*√n -- 1, and so on. All queries within a block are sorted in increasing order of R values.
-
Process all queries one by one in a way that every query uses sum computed in previous query.
- Let 'sum' be sum of previous query.
- Remove extra elements of previous query. For example if previous query is [0, 8] and current query is [3, 9], then we subtract a[0] and a[1] from sum
- Add new elements of current query. In the same example as above, we add a[9] to sum.
The great thing about this algorithm is, in step 2, index variable for R change at mostO(n * √n)times throughout the run and same for L changes its value at mostO(m * √n)times (See below, after the code, for details). All these bounds are possible only because sorted queries first in blocks of√nsize.
The preprocessing part takes O(m Log m) time.
Processing all queries takesO(n * √n)+O(m * √n)=**O((m+n) * √n)**time.
More
https://www.geeksforgeeks.org/range-minimum-query-for-static-array
https://www.geeksforgeeks.org/segment-tree-set-1-range-minimum-query
https://www.geeksforgeeks.org/mos-algorithm-query-square-root-decomposition-set-1-introduction
https://cp-algorithms.com/data_structures/sqrt_decomposition.html
https://www.geeksforgeeks.org/sqrt-square-root-decomposition-technique-set-1-introduction