Ford-Fulkerson Algorithm

Maximum Flow (Max-Flow Min-Cut Theorem)

Network Flow

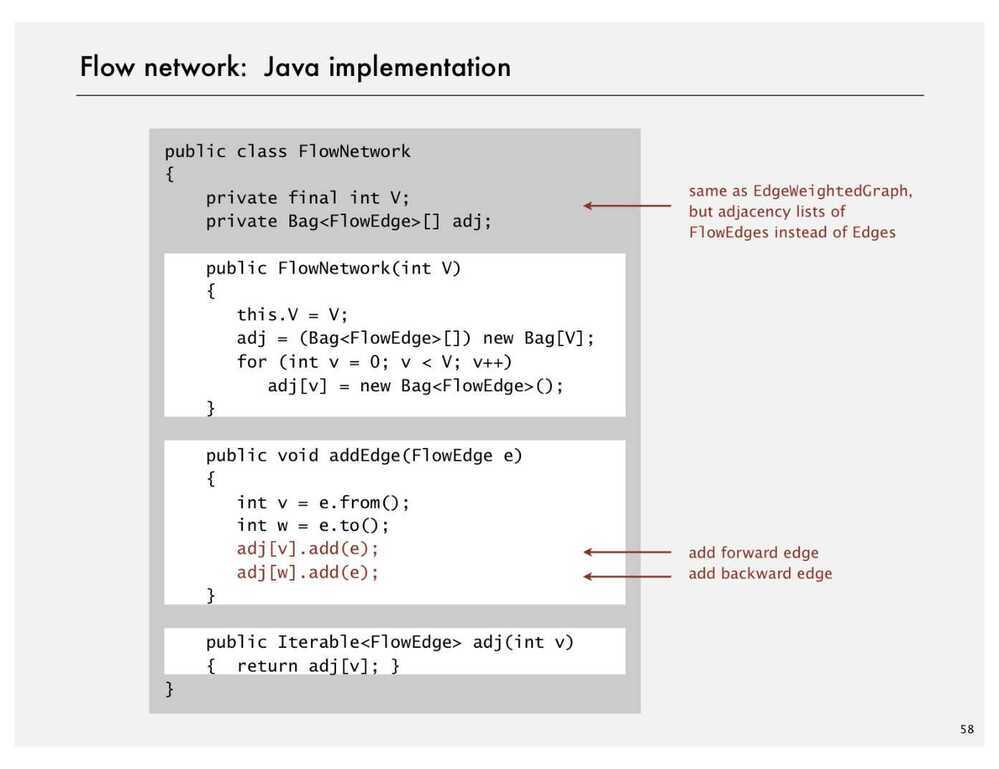
Flow network is a directed graph G=(V,E) such that each

edge has a non-negative capacity c(u,v)≥0.

Two distinguished vertices exist in G namely :

• Source (denoted by s) : In-degree of this vertex is 0.
• Sink (denoted by t) : Out-degree of this vertex is 0.

Flow in a network is an integer-valued function f defined

On the edges of G satisfying 0≤f(u,v)≤c(u,v), for every

Edge (u,v) in E.

• Each edge (u,v) has a non-negative capacity c(u,v).
• If (u,v) is not in E assume c(u,v)=0.
• We have source s and sink t.
• Assume that every vertex v in V is on some path from s to t.

Following is an illustration of a network flow:

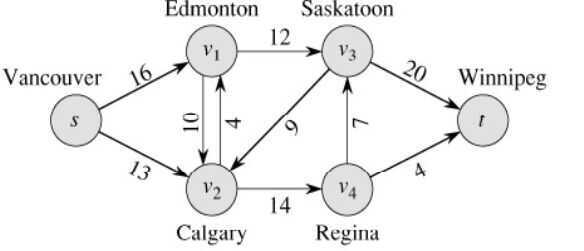
c(s,v1)=16

c(v1,s)=0

c(v2,s)=0 ...

Condition for Network Flow

For each edge (u,v) in E, the flow f(u,v) is a real valued function

that must satisfy following 3 conditions :

• Capacity Constraint : **∀**u,v **∈**V, f(u,v) **≤**c(u,v)
• Skew Symmetry : **∀**u,v **∈**V, f(u,v)= -f(v,u)
• Flow Conservation: **∀**u **∈**V -- {s,t} Σ f(s,v)=0

v∈V

Skew symmetry condition implies that f(u,u)=0.

The value of a flow is given by :

The flow into the node is same as flow going out from the node and

thus the flow is conserved. Also the total amount of flow from source

s = total amount of flow into the sink t.

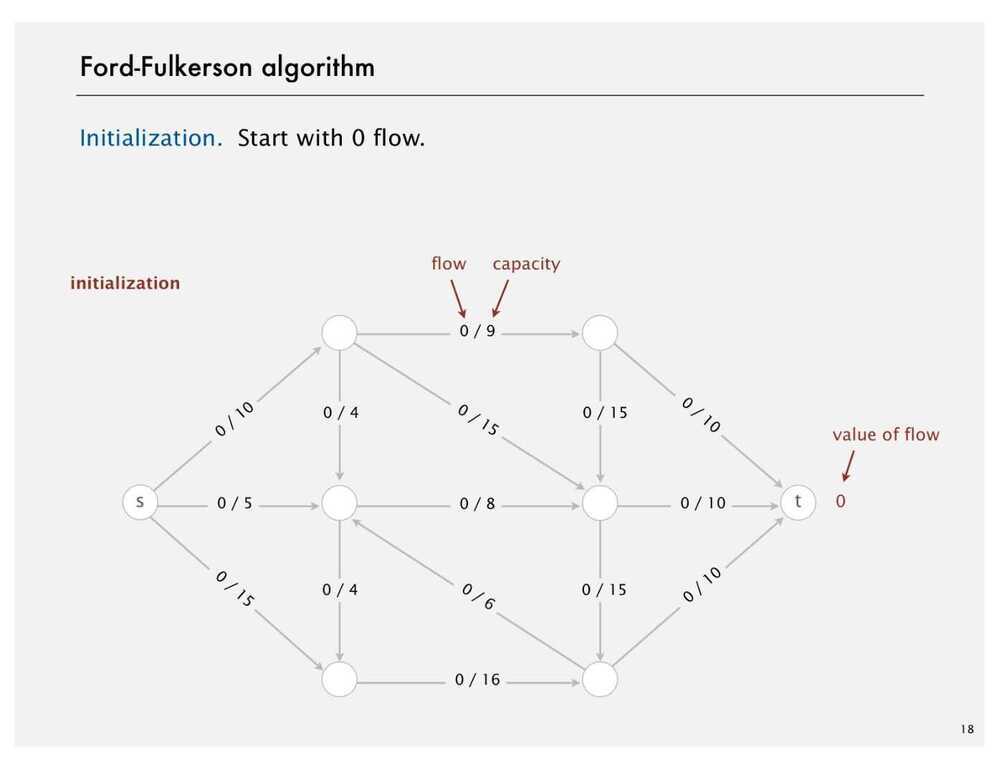
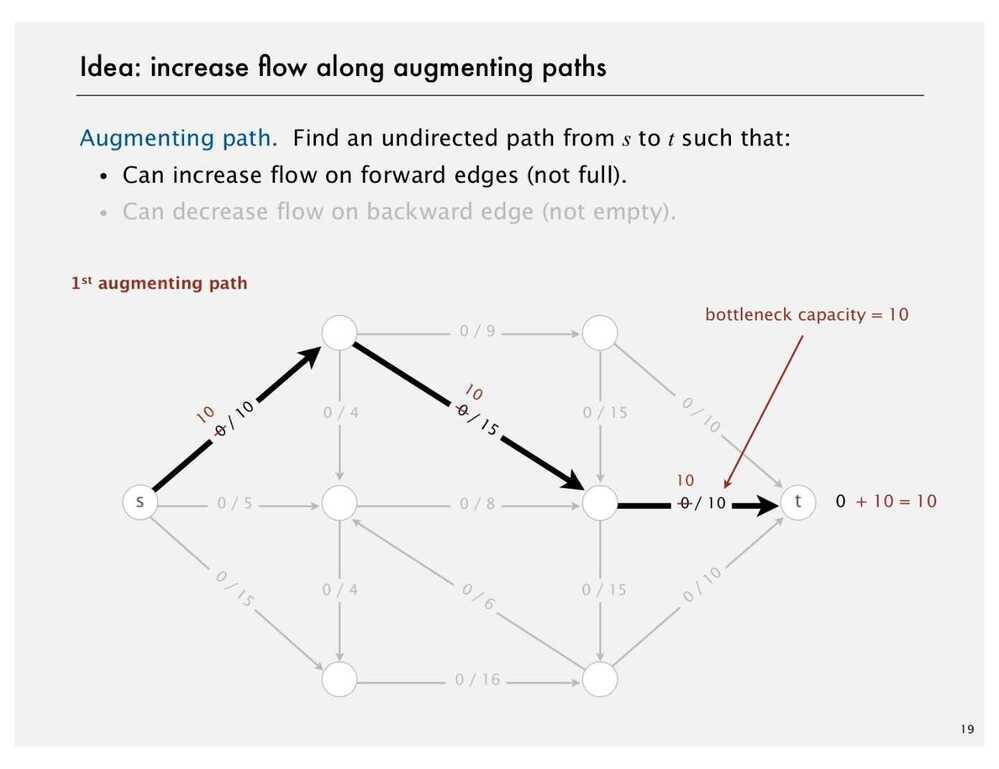
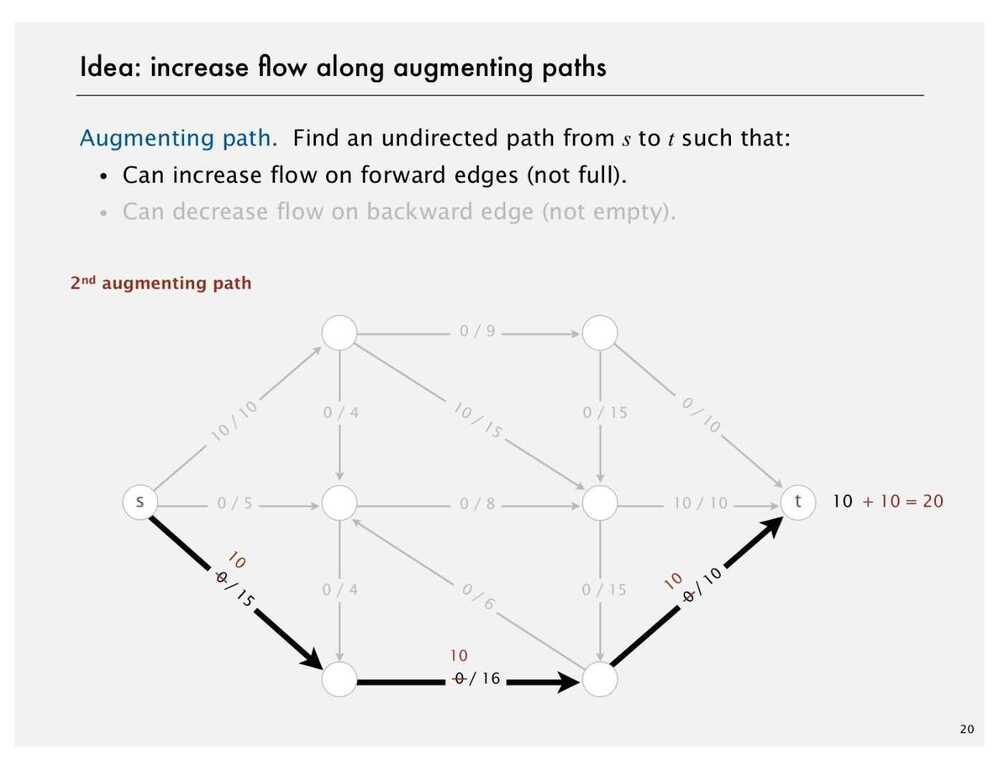
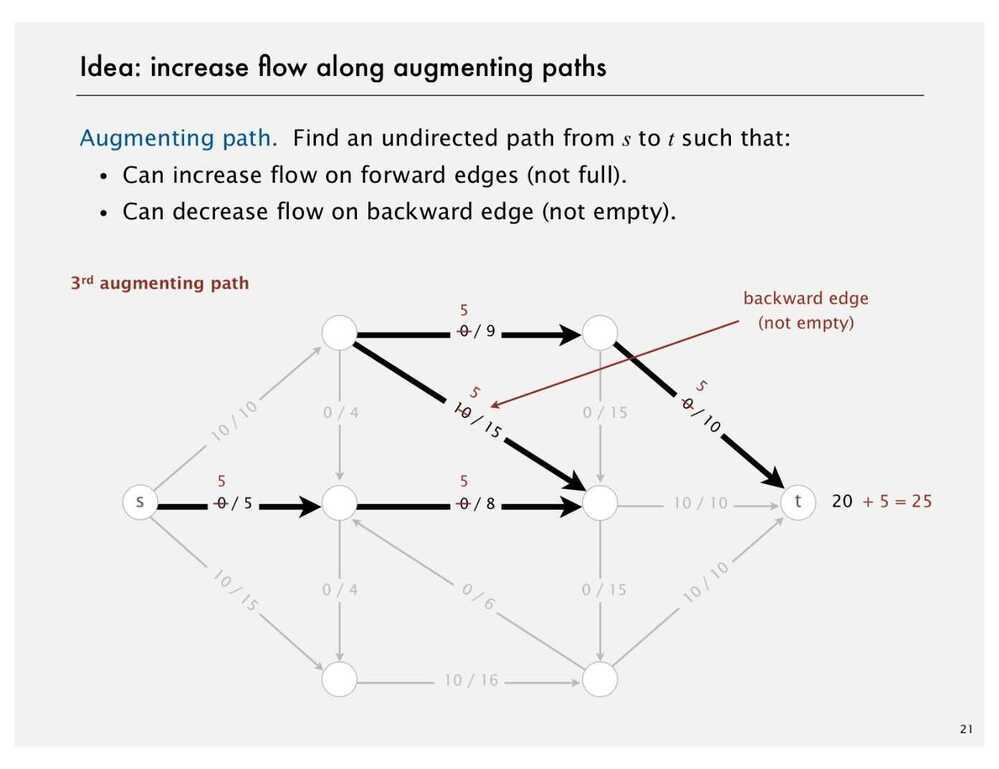
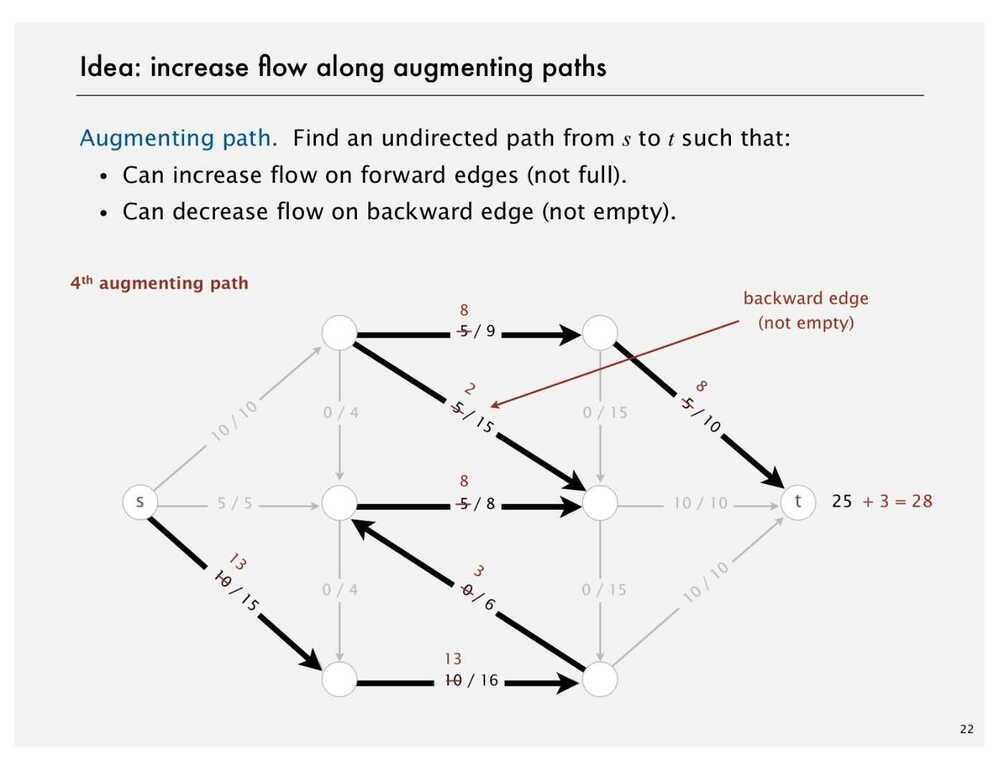
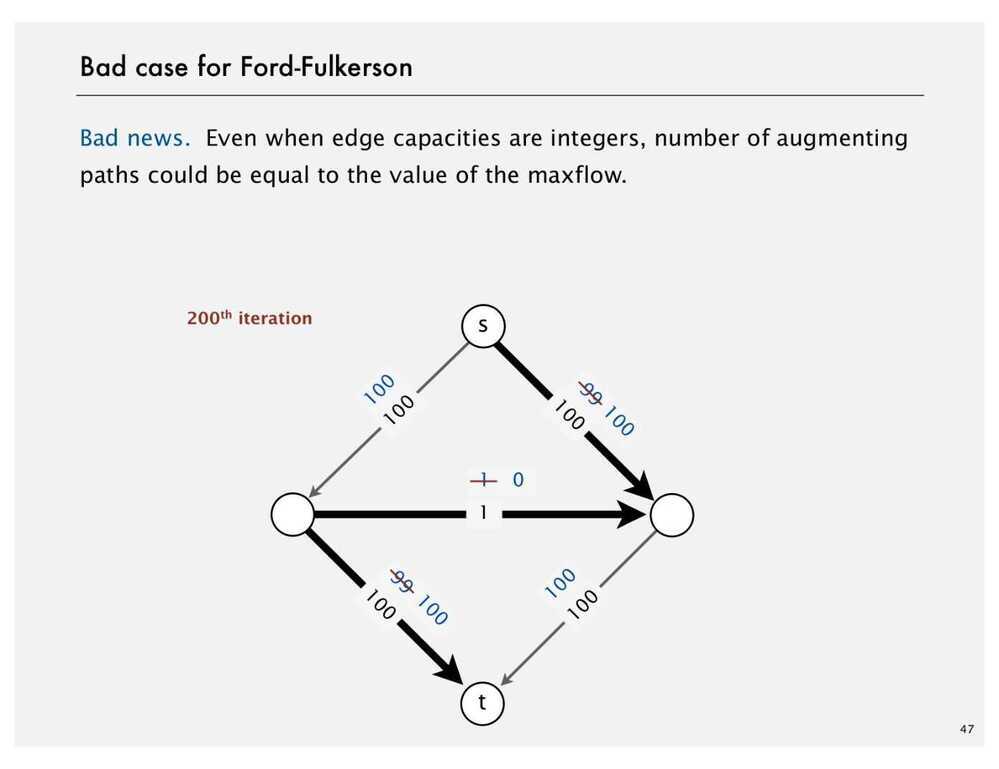
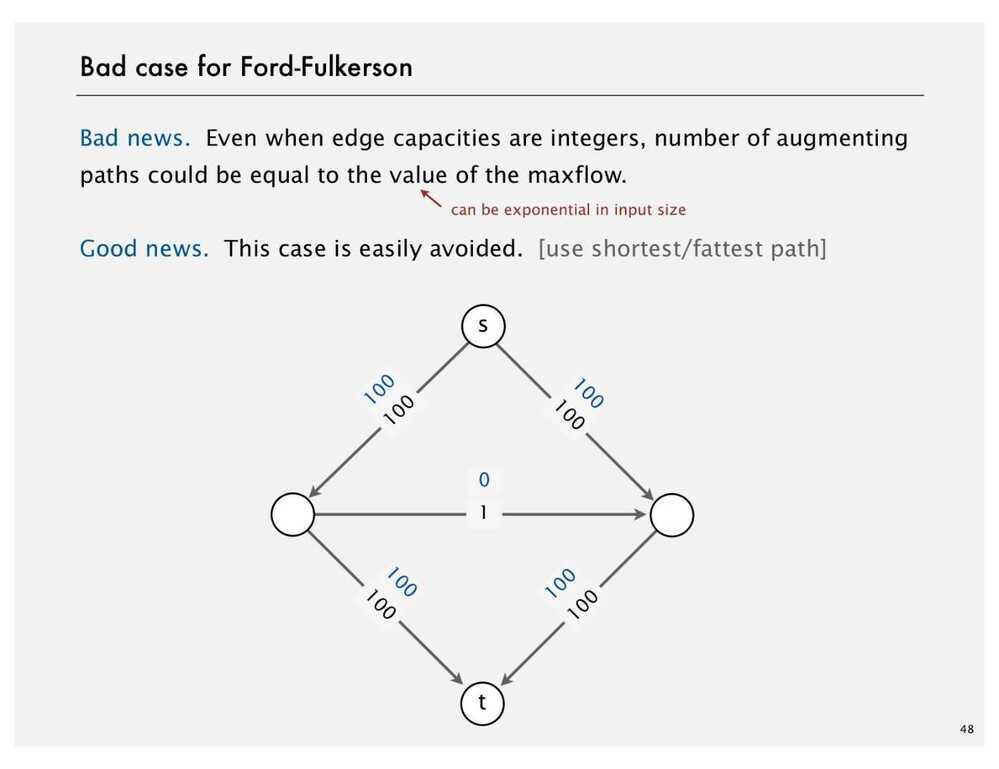
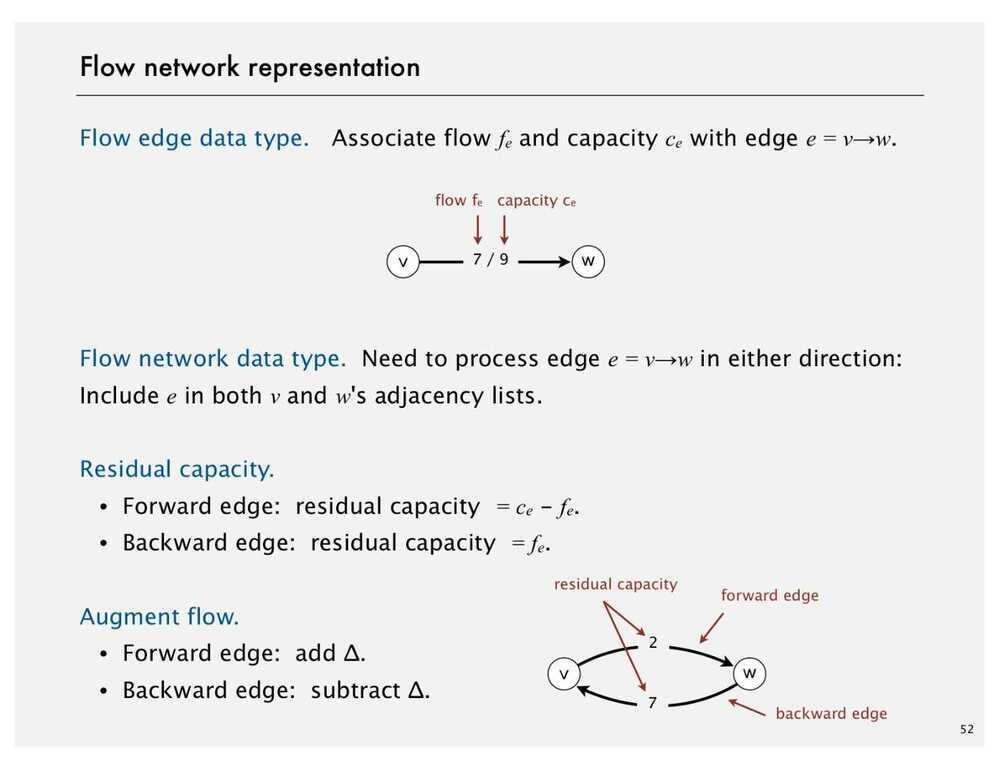
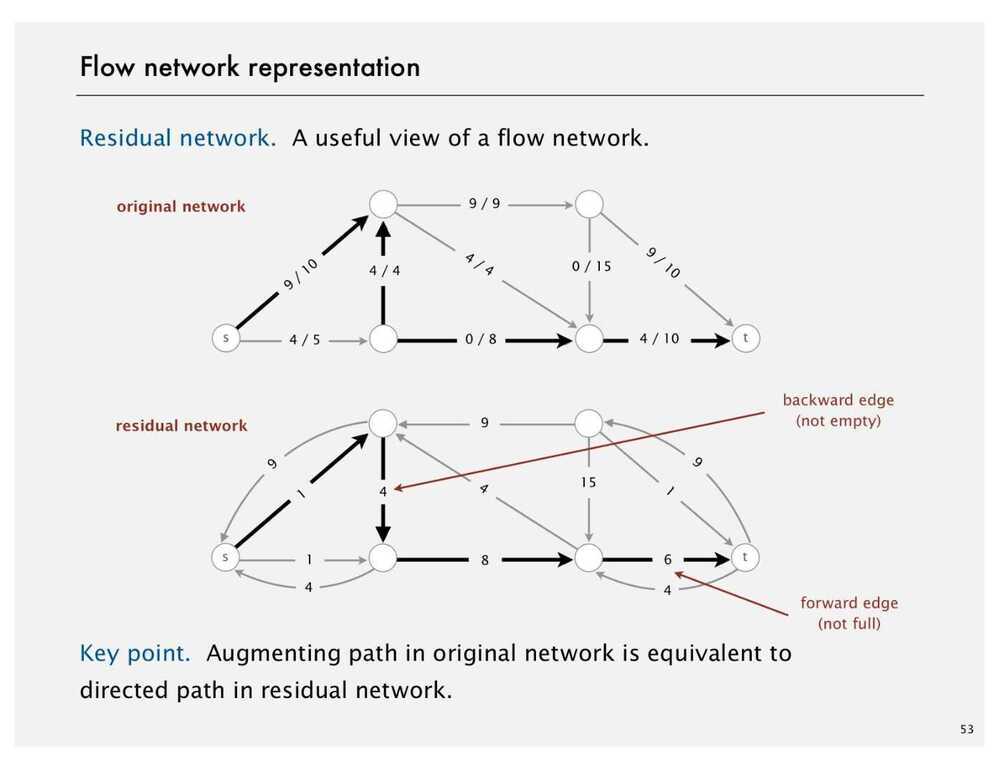
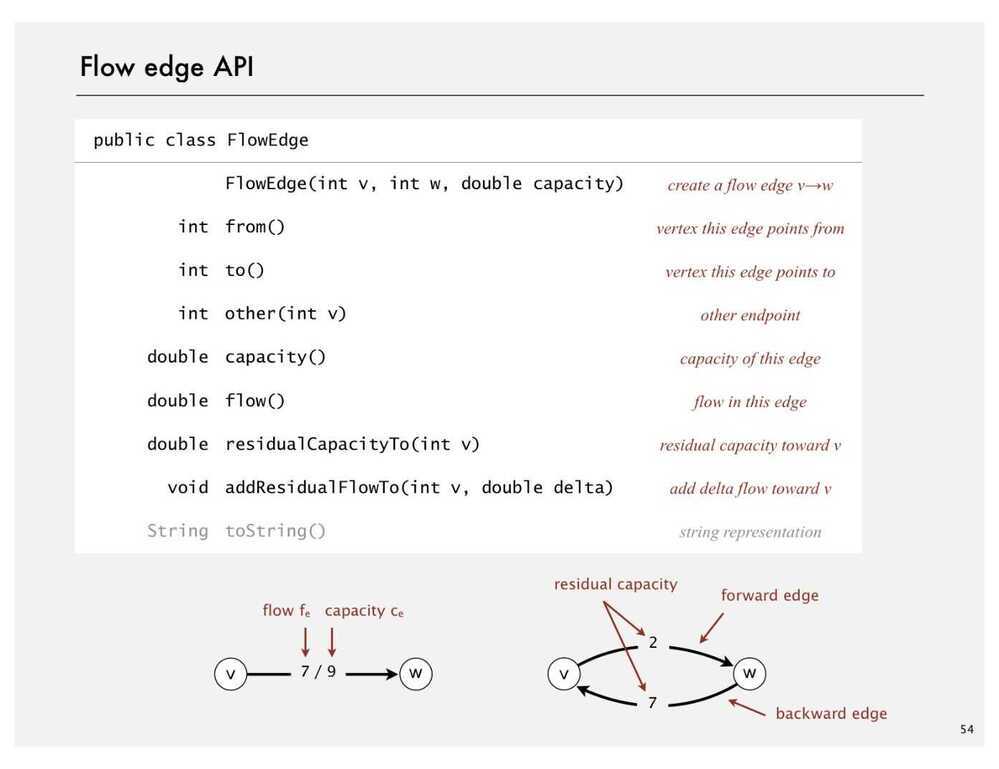
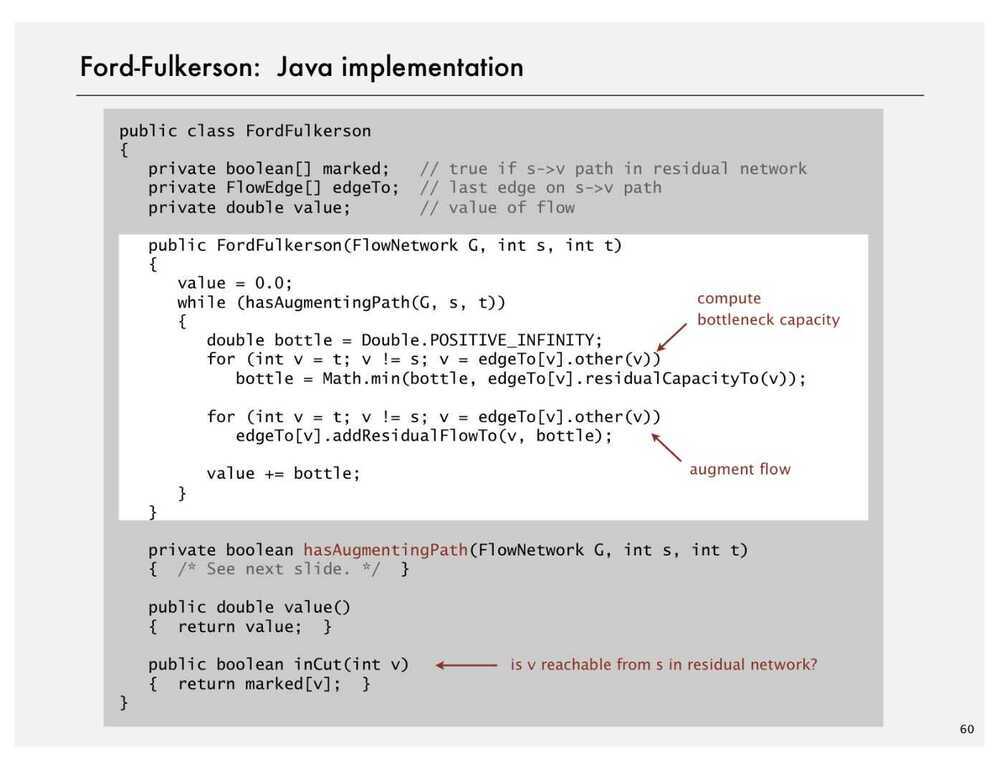
• Create a Residual Graph for finding Augmenting Paths

The maximum amount of flow that we can push through the network does go through the path and find the minimum of either the unused capacity in some forward edge or the available flow in some backward edge. So once we have the bottleneck capacity, then we just go back through the path again and addResidualFlow to every edge in that path.

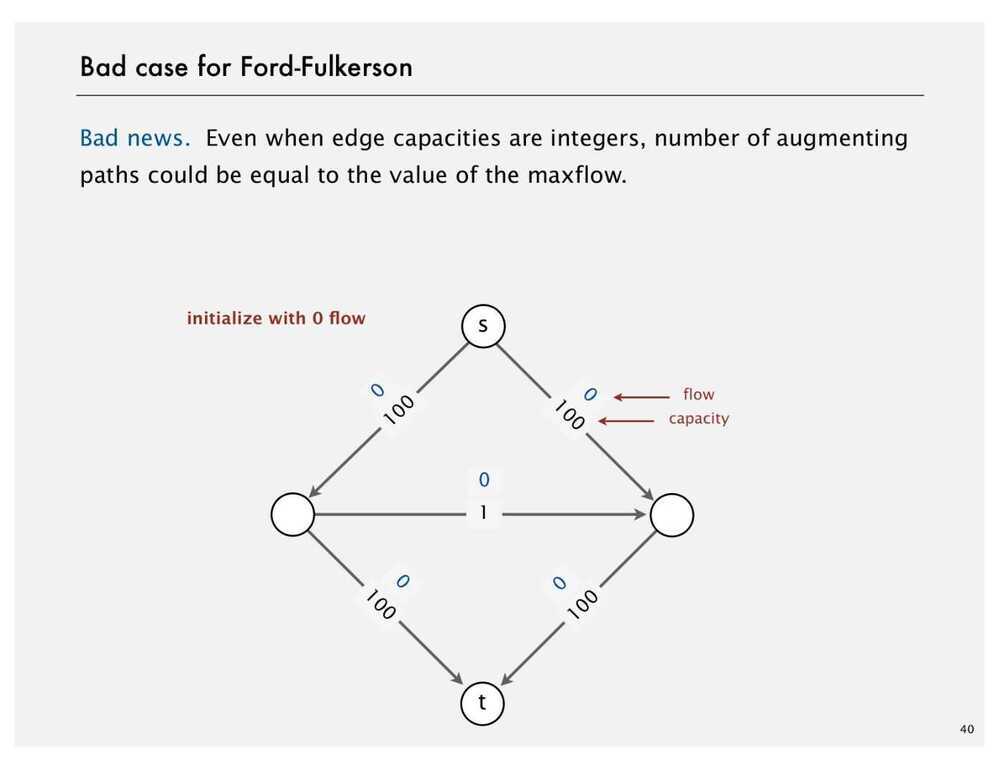
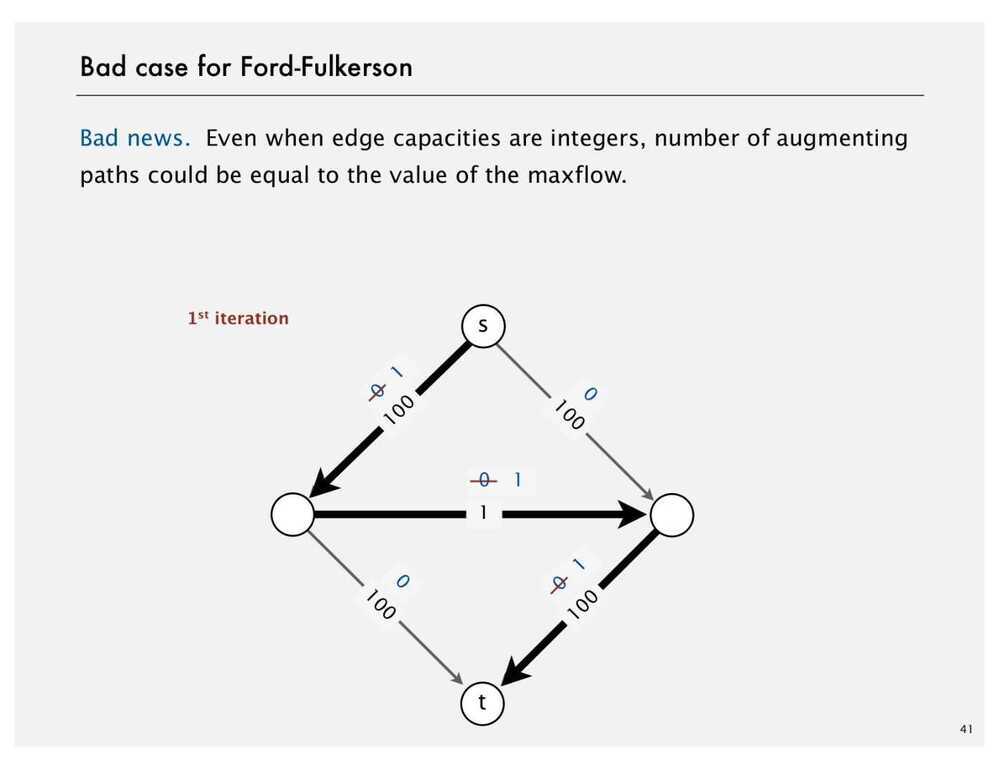
Ford Fulkerson Algorithm

• Try to improve the flow, until we reach the maximum value of the flow

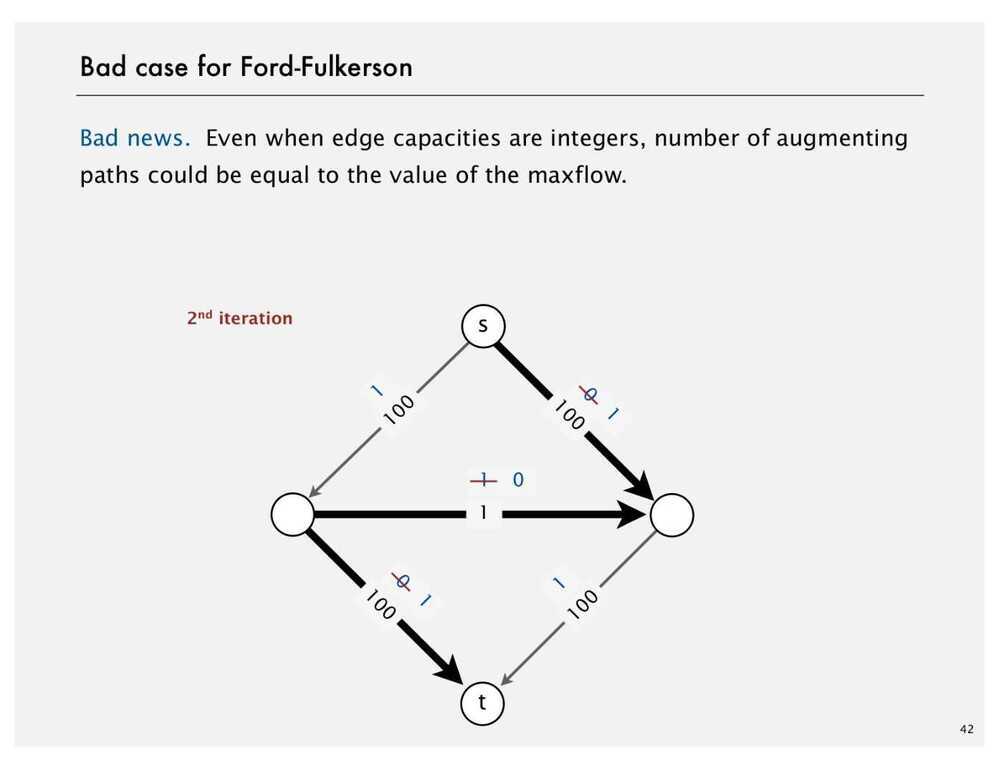
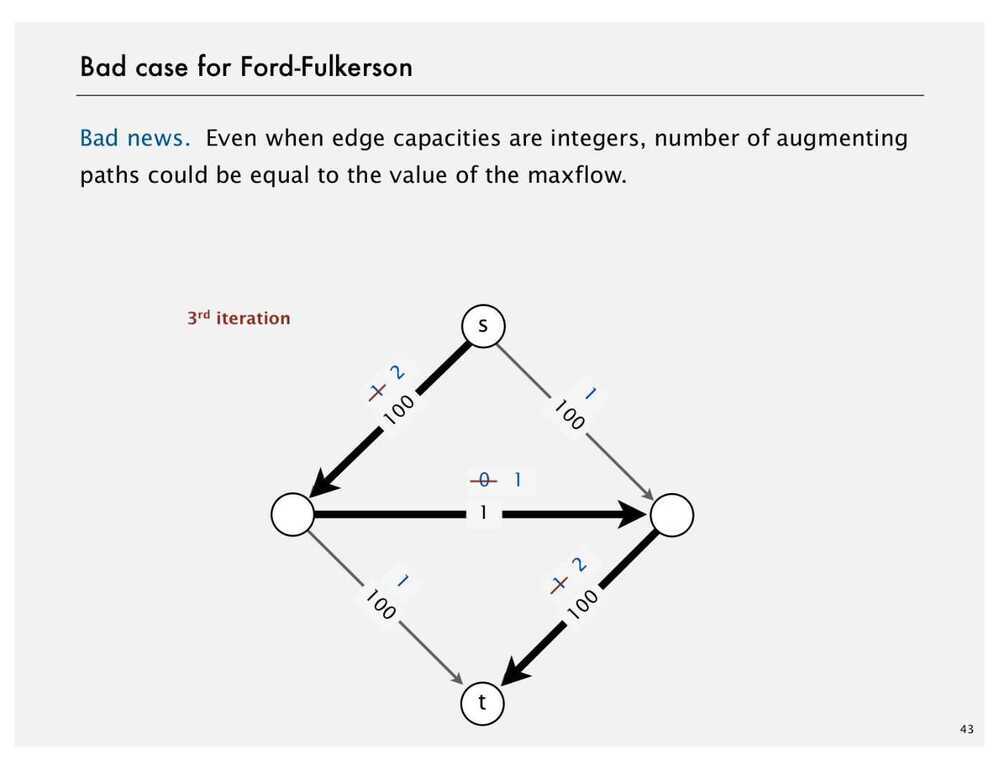
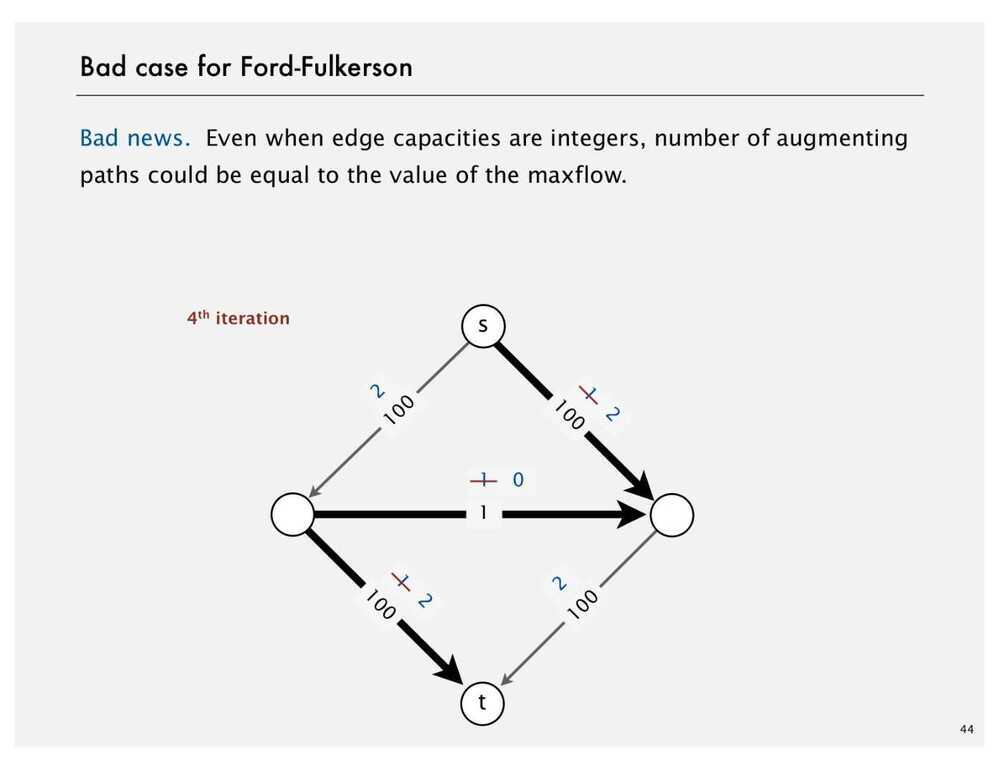
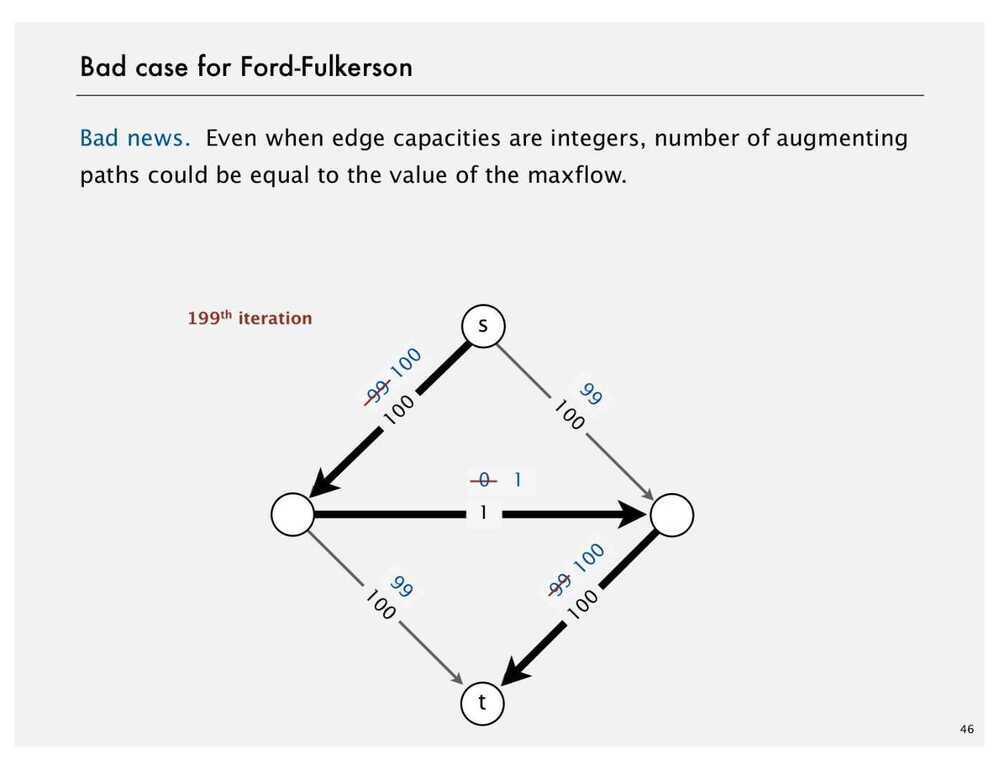
See Also

Edmonds - Karp Algorithm (fully defined version of Ford-Fulkerson Algorithm)