Skip to main content

Huffman Compression

Variable-length codes​

Use different number of bits to encode different chars

image

Que: How do we avoid ambiguity?

Ans: Ensure that no condeword is a prefix of another

Ex 1: Fixed-length code

Ex 2: Append special stop char to each codeword

Ex 3: General prefix-free code

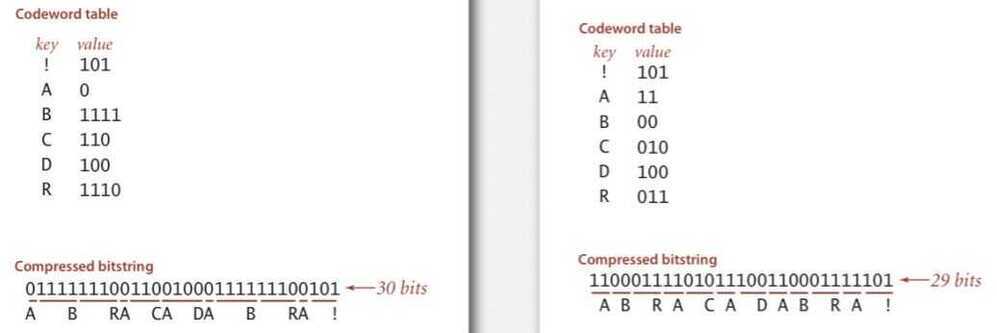
image

Prefix-free codes: trie representation​

Que: How to represent the prefix-free code?

Ans: A binary trie

  • Chars in leaves
  • Codeword is path from root to leaf

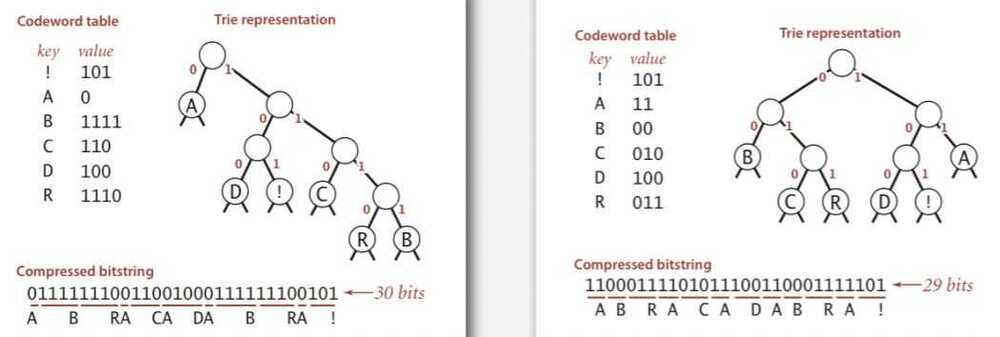
image

Compression​

  • Method 1: start at leaf; follow path up to the root; print bits in reverse
  • Method 2: create ST of key-value pairs

Expansion​

  • Start at root
  • Go left if bit is 0; go right if 1
  • If leaf node, print char and return to root

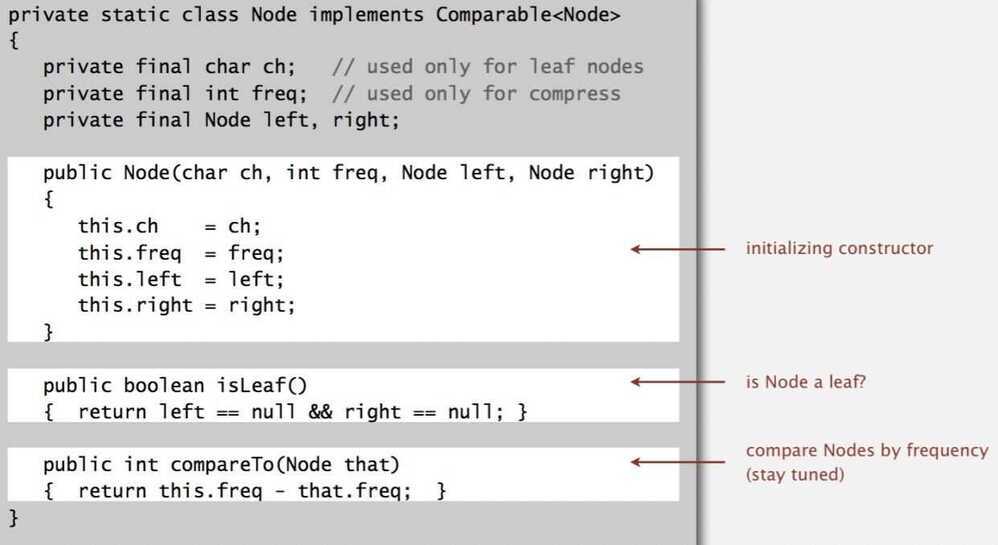
Huffman trie node data type​

image

Prefix-free codes: expansion​

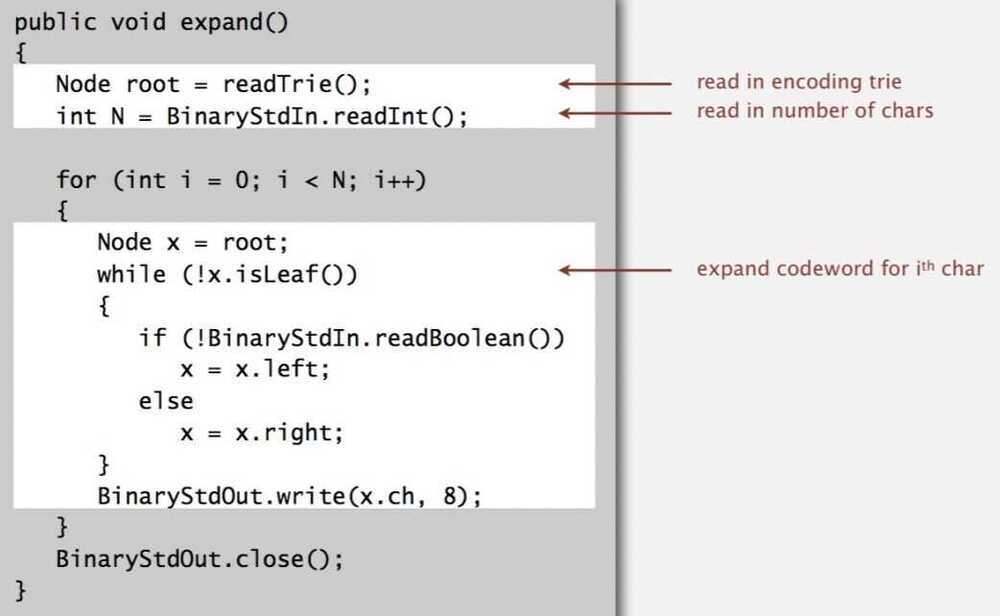
image

Running time: Linear in input size N

How to transmit​

Que: How to write the trie?

Ans: Write preorder traversal of trie; mark leaf and internal nodes with a bit

image

Note: If message is long, overhead of transmitting trie is small

Que: How to read in the trie?

Ans: Reconstruct from preorder traversal of trie

image

Shannon-Fano codes​

Que: How to find best prefix-free code?

Shannon-Fano algorithm:

  • Partition symbols S into two subsets S0 and S1 of (roughly) equal freq
  • Codewords for symbols in S0 start with 0; for symbols in S1 start with 1
  • Recur in S0 and S1.

image

Problem 1: How to divide up symbols?

Problem 2: Not optimal

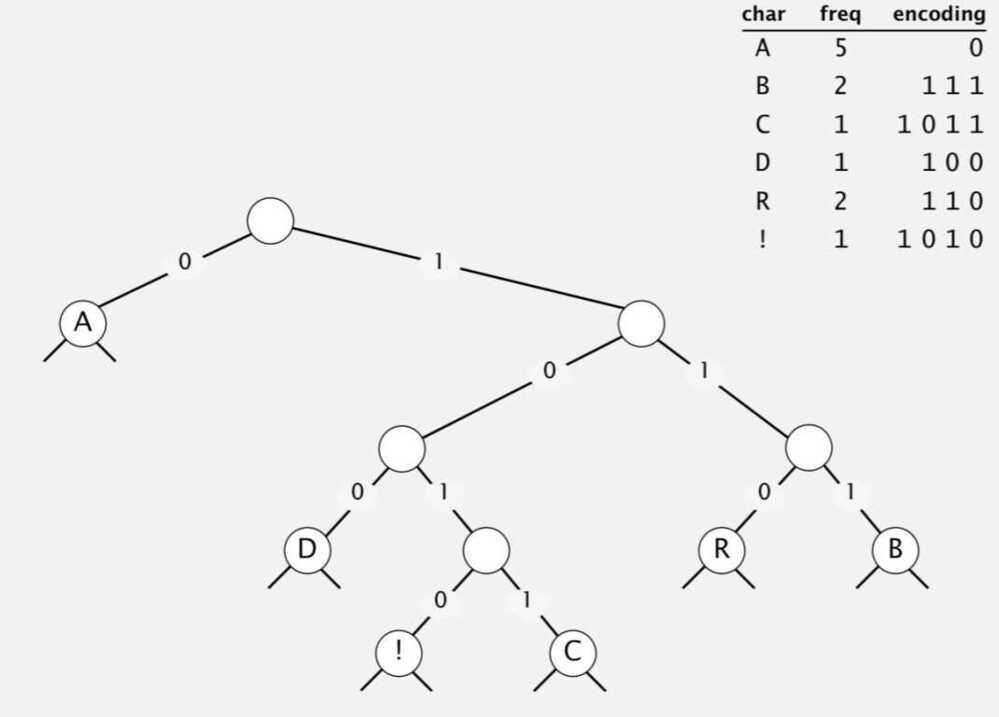
image

Huffman codes​

Que: How to find best prefix-free code?

Huffman algorithm:

  • Count frequency freq[i] for each char i in input
  • Start with one node corresponding to each char i (with weight freq[i])
  • Repeat until single trie formed:
    • Select two tries with min weight freq[i] and freq[j]
    • merge into single trie with weight freq[i] + freq[j]

Constructing a Huffman encoding trie: Java implementation​

image

Huffman encoding summary​

Proposition: Huffman algorithm produces an optimal prefix-free code

Implementation:

Pass 1: tabulate char frequencies and build trie

Pass 2: encode file by traversing frie or lookup table

Running time: Using a binary heap => N+R log R

image